Vẽ tam giác ABC biết \(\widehat{B}=90^0;BC=2cm,\widehat{C}=60^0\). Sau đó đo AC để kiểm tra rằng AC = 4cm ?
Bài 5: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
Bài 49 (Sách bài tập - tập 1 - trang 144)
Thảo luận (2)
Bài 50 (Sách bài tập - tập 1 - trang 144)
Tìm các tam giác bằng nhau trên hình 55 (không xét các tam giác mà các cạnh chưa được kẻ)
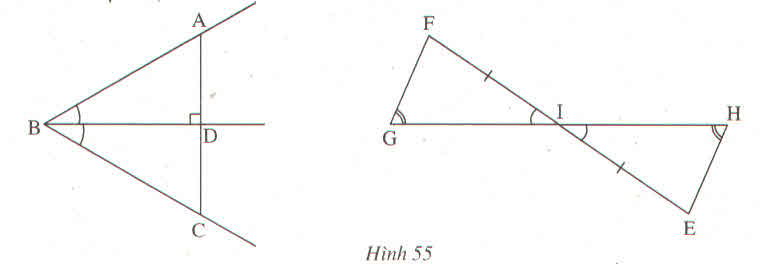
Thảo luận (1)Hướng dẫn giải-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH
(Trả lời bởi Trương Hồng Hạnh)
Bài 51 (Sách bài tập - tập 1 - trang 144)
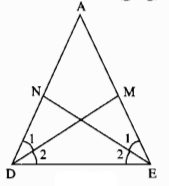
Cho tam giác ADE có \(\widehat{D}=\widehat{E}\). Tia phân giác của góc D cắt AE ở điểm M. Tia phân giác của góc E cắt AD ở điểm N. So sánh các độ dài DN và EM ?
Thảo luận (1)Hướng dẫn giải
Tam giác ADE có: \(\widehat{\text{D}}=\widehat{E}\)(gt)
\(\widehat{\text{D1}}=\widehat{D2}=\dfrac{1}{2}\widehat{D}\)(Vì DM là tia phân giác)
\(\widehat{\text{E1}}=\widehat{E2}=\dfrac{1}{2}\widehat{E}\)(Vì EN là tia phân giác)
Suy ra:\(\widehat{\text{D1}}=\widehat{D2}=\)\(\widehat{\text{E1}}=\widehat{E2}\)
Xét ∆DNE = ∆EMD, ta có:
\(\widehat{NDE}\widehat{=MED}\)((gt)
DE cạnh chung
\(\widehat{\text{D1}}=\widehat{E2}=\)(chứng minh trên)
Suy ra: ∆DNE = ∆EMD (g.c.g)
Vậy DE = EM (2 cạnh tương ứng).
(Trả lời bởi Thảo Phương)
Bài 52 (Sách bài tập - tập 1 - trang 144)
Cho hình 56.
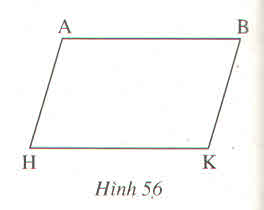
Trong đó AB // HK, AH // BK. Chứng minh rằng AB = HK, AH = BK ?
Thảo luận (3)Hướng dẫn giảiNối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
(Trả lời bởi Trương Hồng Hạnh)
Bài 53 (Sách bài tập - tập 1 - trang 144)
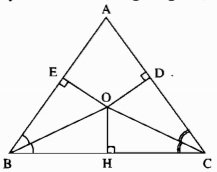
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở O. Kẻ \(OD\perp AC;OE\perp AB\).
Chứng minh rằng OD = OE ?
Thảo luận (1)Hướng dẫn giảiGiải
Kẻ OH⊥BC
Xét hai tam giác vuông OEB và OHB, ta có:
\(\widehat{\text{OEB}}=\widehat{\text{OHB}}\)=90o
Cạnh huyền OB chung
\(\widehat{EBO}=\widehat{\text{HB}O}\)(gt)
Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)
⇒ OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
\(\widehat{\text{OHC}}=\widehat{\text{ODC}}\)=90oCạnh huyền OC chung
\(\widehat{\text{HCO}}=\widehat{\text{DCO}}\)(gt)
Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)
⇒ OH = OD (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD.
(Trả lời bởi Thảo Phương)
Bài 54 (Sách bài tập - tập 1 - trang 144)
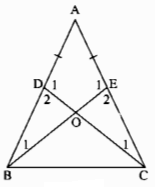
Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE
a) Chứng minh rằng BE = CD
b) Gọi O là giao điểm của BE và CD. Chứng minh rằng \(\Delta BOD=\Delta COE\)
Thảo luận (1)Hướng dẫn giải
a) Xét ∆BEA và ∆CDA, ta có:
BA = CA (gt)
\(\widehat{A}\)chung
AE = AD (gt)
Suy ra: ∆BEA = ∆CDA (c.g.c)
Vậy BE = CD (hai cạnh tương ứng)
b) ∆BEA = ∆CDA (chứng minh trên)
⇒\(\widehat{\text{B1}}=\widehat{\text{C1}}\);\(\widehat{\text{E1}}=\widehat{\text{D1}}\) (hai góc tương ứng)
\(\widehat{\text{E1}}+\widehat{\text{E2}}\)=180o (hai góc kề bù)
\(\widehat{\text{D1}}+\widehat{\text{D2}}\)=180o (hai góc kề bù)
Suy ra: \(\widehat{\text{E2}}=\widehat{\text{D2}}\)
AB = AC (gt)
⇒ AE + EC = AD + DB mà AE = AD (gt) => EC = DB
Xét ∆ODB và ∆OCE, ta có:
\(\widehat{\text{E2}}=\widehat{\text{D2}}\) (chứng minh trên)
DB = EC (chứng minh trên)
\(\widehat{\text{B1}}=\widehat{\text{C1}}\)(chứng minh trên)
Suy ra: ∆ODB = ∆OEC (g.c.g)
(Trả lời bởi Thảo Phương)
Bài 55 (Sách bài tập - tập 1 - trang 145)
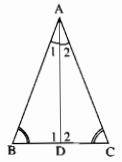
Cho tam giác ABC có \(\widehat{B}=\widehat{C}\). Tia phân giác của góc A cắt BC tại D.
Chứng minh rằng :
DB = DC; AB = AC
Thảo luận (2)Hướng dẫn giảiGiải
Trong ∆ADB, ta có:
\(\widehat{\text{B}}+\widehat{A1}+\widehat{D1}\)=180o(tổng ba góc trong tam giác)
Suy ra: \(\widehat{D1}\)=180o−(\(\widehat{\text{B}}+\widehat{A1}\)) (1)
Trong ∆ADC, ta có:
\(C+\widehat{A2}+\widehat{D2}\)=180o(tổng ba góc trong tam giác)
Suy ra:\(\widehat{D2}\)=180o−\((C+\widehat{A2})\) (2)
\(\widehat{B}=\widehat{C}\)(gt)
\(\widehat{A1}=\widehat{A2}\) (gt)
Từ (1), (2) và (gt) suy ra: \(\widehat{D1}=\widehat{D2}\)
Xét ∆ADB và ∆ADC, ta có:
\(\widehat{A1}=\widehat{A2}\)
AD cạnh chung
\(\widehat{D1}=\widehat{D2}\) (chứng minh trên)
Suy ra: ∆ADB = ∆ADC(g.c.g)
Vậy: AB = AC (2 cạnh tương ứng)
DB = DC (2 cạnh tương ứng)
(Trả lời bởi Thảo Phương)
Bài 56 (Sách bài tập - tập 1 - trang 145)
Cho hình 57, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC
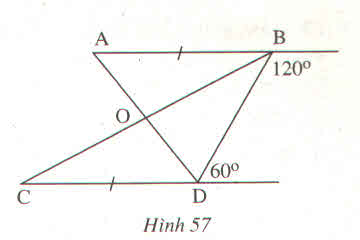
Thảo luận (1)Hướng dẫn giảiTa có: góc B + góc D = 1200 + 600 = 1800
Mà hai góc này TCP
=> AB // CD
Xét tam giác ABO và tam giác CDO có:
AB = CD (GT)
ABC = BCD (AB // CD)
BAD = ADC (AB // CD)
=> tam giác ABO = tam giác CDO
=> AO = OD
=> O là trung điểm AD
Ta có: tam giác ABO = tam giác CDO
=> BO = OC
=> O là trung điểm BC
(Trả lời bởi Trương Hồng Hạnh)
Bài 57 (Sách bài tập - tập 1 - trang 145)
Cho hình 58.
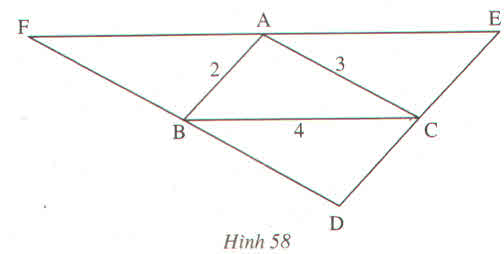
Trong đó DE // AB, DF // AC, EF // BC
Tính chu vi tam giác DEF ?
Thảo luận (1)Hướng dẫn giảigiải
*xét tam giác abc và tam giác abf có
góc abc=góc bà(so le trong)
ad;chung
góc bac=góc abf(so le trong)
suy ra tam giác abc=tam giác abf(gcg)
suy ra af=bc=4(2 cạnh tương ứng)
bf=ac=3
*xét tam giác abc và tam giác ace có
góc acb=góc cae(số lẻ trong)
ac; chung
gốc bac= gốc eca(slt)
suy ra tam giác abc= tam giác ace
suy ra ae=bc=4(2 cạnh tương ứng)
ce=ab=2
* xét tam giác abc và tam giác dcb có
góc acb= góc dbc(slt)
bc;chung
góc abc= góc dcb
suy ra tam giác abc=tam giác dcb
suy ra dc=ab=2
db=ac=3
ta có ef=ae+af=4+4=8
df=db+bf=3+3=6
de=dc+ce=2+2=4
vậy chu vi của tam giác def là
để+DF+EF=4+6+8=18(ĐƠN VỊ ĐO ĐỘ DÀI)
(Trả lời bởi nguyen thi thao)
Bài 58 (Sách bài tập - tập 1 - trang 145)
Cho đoạn thẳng AB. Qua A vẽ đường thẳng m vuông góc với AB. Qua B vẽ đường thẳng n vuông góc với AB. Qua trung điểm O của AB vẽ một đường thẳng cắt m ở C và cắt n ở D. So sánh các độ dài OC và OD ?
Thảo luận (1)Hướng dẫn giải