Giải
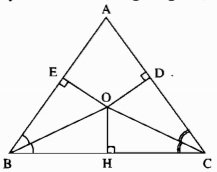
Kẻ OH⊥BC
Xét hai tam giác vuông OEB và OHB, ta có:
\(\widehat{\text{OEB}}=\widehat{\text{OHB}}\)=90o
Cạnh huyền OB chung
\(\widehat{EBO}=\widehat{\text{HB}O}\)(gt)
Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)
⇒ OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
\(\widehat{\text{OHC}}=\widehat{\text{ODC}}\)=90oCạnh huyền OC chung
\(\widehat{\text{HCO}}=\widehat{\text{DCO}}\)(gt)
Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)
⇒ OH = OD (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD.
Đúng 1
Bình luận (0)
