Giải
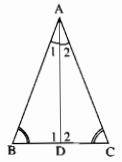
Trong ∆ADB, ta có:
\(\widehat{\text{B}}+\widehat{A1}+\widehat{D1}\)=180o(tổng ba góc trong tam giác)
Suy ra: \(\widehat{D1}\)=180o−(\(\widehat{\text{B}}+\widehat{A1}\)) (1)
Trong ∆ADC, ta có:
\(C+\widehat{A2}+\widehat{D2}\)=180o(tổng ba góc trong tam giác)
Suy ra:\(\widehat{D2}\)=180o−\((C+\widehat{A2})\) (2)
\(\widehat{B}=\widehat{C}\)(gt)
\(\widehat{A1}=\widehat{A2}\) (gt)
Từ (1), (2) và (gt) suy ra: \(\widehat{D1}=\widehat{D2}\)
Xét ∆ADB và ∆ADC, ta có:
\(\widehat{A1}=\widehat{A2}\)
AD cạnh chung
\(\widehat{D1}=\widehat{D2}\) (chứng minh trên)
Suy ra: ∆ADB = ∆ADC(g.c.g)
Vậy: AB = AC (2 cạnh tương ứng)
DB = DC (2 cạnh tương ứng)
Giải
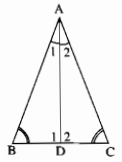
Trong ∆ADB, ta có:
ˆB+ˆA1+ˆD1=180∘B^+A1^+D1^=180∘ (tổng ba góc trong tam giác)
Suy ra: ˆD1=180∘–(ˆB+ˆA1)D1^=180∘–(B^+A1^) (1)
Trong ∆ADC, ta có:
ˆC+ˆD2+ˆA2=180∘C^+D2^+A2^=180∘ (tổng ba góc trong tam giác)
Suy ra: ˆD2=180∘–(ˆC+ˆA2)D2^=180∘–(C^+A2^) (2)
ˆB=ˆC(gt)B^=C^(gt)
ˆA1=ˆA2(gt)A1^=A2^(gt)
ˆB=ˆC(gt)B^=C^(gt)
Từ (1), (2) và (gt) suy ra: ˆD1=ˆD2D1^=D2^
Xét ∆ADB và ∆ADC, ta có:
ˆA1=ˆA2A1^=A2^
AD cạnh chung
ˆD1=ˆD2D1^=D2^ (chứng minh trên)
Suy ra: ∆ADB = ∆ADC(g.c.g)
Vậy: AB = AC (2 cạnh tương ứng)
DB = DC (2 cạnh tương ứng)










