Bài 5: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
Các câu hỏi tương tự
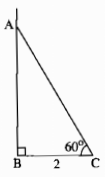
Vẽ tam giác ABC biết \(AC=2cm,\widehat{A}=90^0,\widehat{C}=60^0\) ?
Cho tam giác ABC có widehat{A}90^0 (h.109). Kẻ AH vuông góc với BC (Hin BC ). Các tam giác AHC và BAC có AC là cạnh chung. widehat{C} là góc chung, widehat{AHC}widehat{BAC}90^0, nhưng hai tam giác đó không bằng nhau
Tại sao ở đây không thể áp dụng trường hợp góc - cạnh - góc để kết luận Delta AHCDelta BAC ?
Đọc tiếp
Cho tam giác ABC có \(\widehat{A}=90^0\) (h.109). Kẻ AH vuông góc với BC (\(H\in BC\) ). Các tam giác AHC và BAC có AC là cạnh chung. \(\widehat{C}\) là góc chung, \(\widehat{AHC}=\widehat{BAC}=90^0\), nhưng hai tam giác đó không bằng nhau
Tại sao ở đây không thể áp dụng trường hợp góc - cạnh - góc để kết luận \(\Delta AHC=\Delta BAC\) ?

Vẽ tam giác ABC biết AC = 2cm, = 90*,C = 60*
Cho tam giác ABC có \(\widehat{A}=60^0\). Các tia phân giác của các góc B, C cắt nhau ở I và cắt AC, AB theo thứ tự ở D, E. Chứng minh rằng ID = IE
Hướng dẫn : Kẻ tia phân giác của góc BIC
Cho tam giác ABC có \(\widehat{B}=\widehat{C}\). Tia phân giác của góc A cắt BC tại D.
Chứng minh rằng :
DB = DC; AB = AC
Cho tam giâc ABC và tam giác có ba đỉnh là D, E, F. Biết AB DF và widehat{B}widehat{D}
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
a) Nếu widehat{A}widehat{F} thì hai tam giác đó bằng nhau
b) Nếu widehat{A}widehat{E} thì hai tam giác đó bằng nhau
c) Nếu widehat{C}widehat{E} thì hai tam giác đó bằng nhau
Đọc tiếp
Cho tam giâc ABC và tam giác có ba đỉnh là D, E, F. Biết AB = DF và \(\widehat{B}=\widehat{D}\)
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
a) Nếu \(\widehat{A}=\widehat{F}\) thì hai tam giác đó bằng nhau
b) Nếu \(\widehat{A}=\widehat{E}\) thì hai tam giác đó bằng nhau
c) Nếu \(\widehat{C}=\widehat{E}\) thì hai tam giác đó bằng nhau
Cho tam giác ABC, có góc C bằng 50 độ. Vẽ BD vuông góc với AC ( D thuộc cạnh AC), vẽ DE song song với BC ( E thuộc cạnh AB). Tính số đo góc BDE
Cho tam giác ABC có góc A = 60 độ. Các tia phân giác của góc B và C lần lượt cắt các cạnh AC và AB tại D và E.
a, Chứng minh BE + CD = BC
b, Gọi I là giao điểm của BD và CE. Tính số đo các góc của tam giác IDE
Cho tam giác ABC có góc A < 90 độ. Trên nửa mặt phẳng bờ AB có chứa điểm C vẽ AD vuông góc với AB và AD = AB, trên nửa mặt phẳng bờ AC có chứa điểm B vẽ AE vuông góc với AC và AE = AC. Kẻ AH vuông góc với ED tia AH cắt BC tại M. chứng minh M là trung điểm của BC