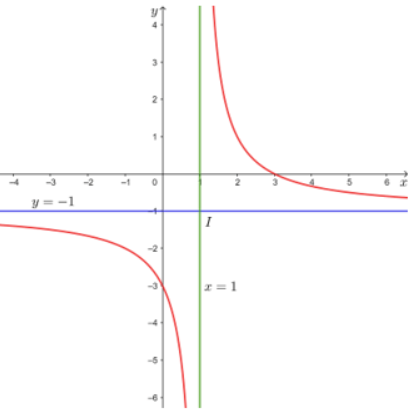
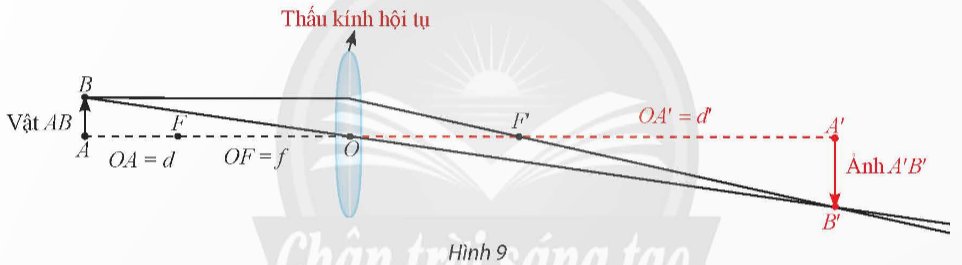
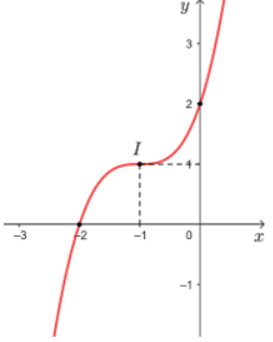
Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f 0. Gọi d là khoảng cách từ vật đến thấu kính (d 0), d là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d 0, ảnh ảo thì d 0). Ta có công thức:dfrac{1}{f}dfrac{1}{d}+dfrac{1}{d} hay ddfrac{df}{d-f}.(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187).Xét trường hợp f 3, đặt x d, y d. Ta có hàm số ydfrac{3x}{x-3} và x ≠ 3.a) Khảo sát và vẽ đồ thị của hàm số trên.b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật đ...
Đọc tiếp
Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d' là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d' > 0, ảnh ảo thì d' < 0). Ta có công thức:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\) hay \(d'=\dfrac{df}{d-f}\).
(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187).
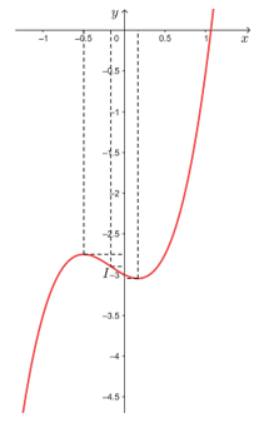
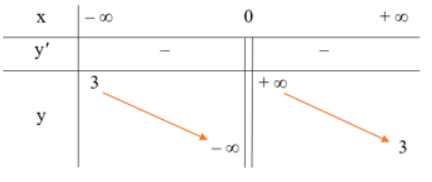
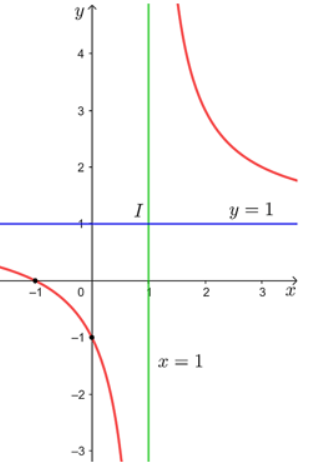
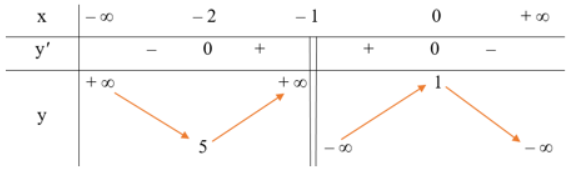
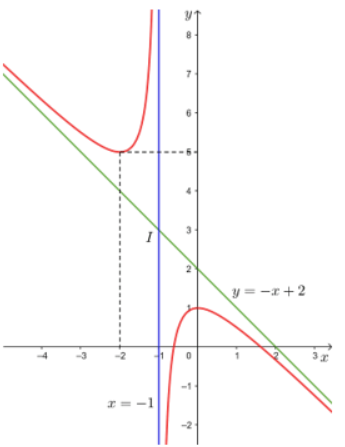
Xét trường hợp f = 3, đặt x = d, y = d'. Ta có hàm số \(y=\dfrac{3x}{x-3}\) và x ≠ 3.
a) Khảo sát và vẽ đồ thị của hàm số trên.
b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo.
c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?
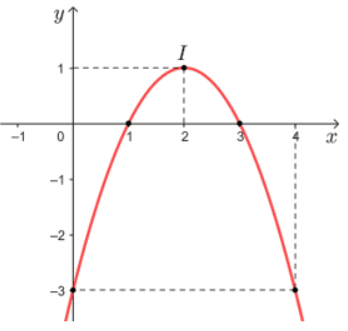
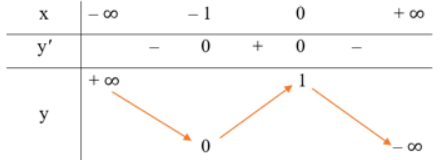
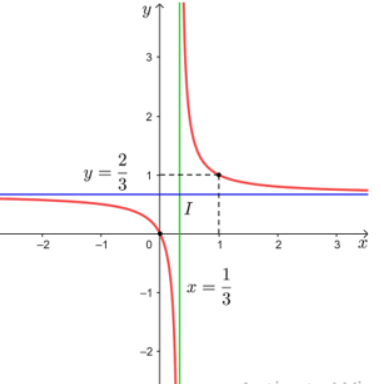
 Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)

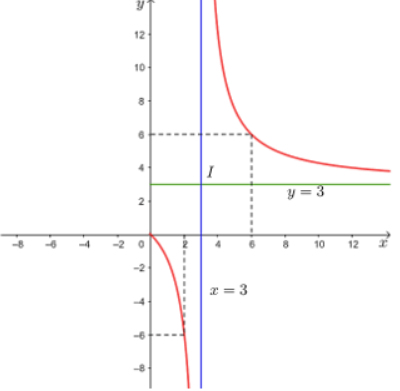
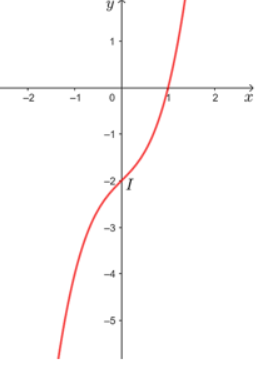
 Khi x = 0 thì y = -3 nên (0; -3) là giao điểm của đồ thị với trục Oy
Khi x = 0 thì y = -3 nên (0; -3) là giao điểm của đồ thị với trục Oy