Bài 4. Góc ở tâm. Góc nội tiếp

Hướng dẫn giải

Ta có: \(\widehat {ACB}\) và \(\widehat {ADB}\) là hai góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \widehat {ADB}\) hay \(\widehat {ACI} = \widehat {BDI}\).

Do \(\widehat {CIA}\) và \(\widehat {DIB}\) là hai góc đối đỉnh nên \(\widehat {CIA} = \widehat {DIB}\).

Xét \(\Delta CIA\) và \(\Delta DIB\) có:

$\left\{ \begin{align}\widehat{ACI}=\widehat{BDI} \\ \widehat{CIA}=\widehat{DIB} \end{align} \right.\Rightarrow \Delta CIA\backsim \Delta DIB\left( g.g \right) \Rightarrow \frac{CI}{DI}=\frac{IA}{IB}\Rightarrow IA.ID=IC.IB.$

(Trả lời bởi datcoder)

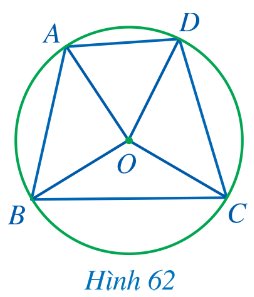
Hướng dẫn giải

a)  6 góc ở tâm có hai cạnh lần lượt chứa hai trong bốn điểm \(A,B,C,D\) là: \(\widehat {AOB};\widehat {AOD};\widehat {AOC};\widehat {DOC};\widehat {DOB};\widehat {COB}\),

b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm là: \(\widehat {BAD};\widehat {ADC};\widehat {DCB};\widehat {CBA}\).

(Trả lời bởi datcoder)

Hướng dẫn giải

a) Áp dụng định lí Pythagore vào tam giác \(AOB\) vuông tại \(O\), ta có:

\(O{A^2} + O{B^2} = A{B^2} \Rightarrow A{B^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AB = R \sqrt 2\)

b) Xét đường tròn \(\left( O \right)\):

+) Vì M thuộc cung lớn AB nên \(\widehat {AMB}\) là góc nội tiếp và \(\widehat {AOB}\) là góc ở tâm cùng chắn cung nhỏ \(AB\) nên:

\(\widehat {AMB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.90^\circ = 45^\circ \).

+) Số đo cung lớn AB là:

$sđ\overset\frown{AB}\; lớn=360{}^\circ - sđ\overset\frown{AB }\; nhỏ=360{}^\circ -90{}^\circ =270{}^\circ $

+) Vì N thuộc cung nhỏ AB nên \(\widehat {ANB}\) là góc nội tiếp chắn cung lớn \(AB\) nên:

$\widehat{ANB}=\frac{1}{2}sđ\overset\frown{AB }\; lớn=\frac{1}{2}.270{}^\circ =135{}^\circ $.

Vậy \(\widehat {AMB} = 45^\circ ,\widehat {ANB} = 135^\circ \).

(Trả lời bởi datcoder)

Hướng dẫn giải

a) Xét tam giác \(OAB\) có: \(OA = OB = AB = R\) nên tam giác \(OAB\) đều.

Vậy \(\widehat {AOB} = 60^\circ \).

b) Xét đường tròn \(\left( O \right)\) có:

+ \(\widehat {AOB}\) là góc ở tâm chắn cung \(AB\) nên $\widehat{AOB}=sđ\overset\frown{AB}=60{}^\circ $

+ $sđ\overset\frown{A{{B}_{lớn}}}=360{}^\circ -sđ\overset\frown{A{{B}_{nhỏ}}}=360{}^\circ -60{}^\circ =300{}^\circ $

c) Xét đường tròn \(\left( O \right)\) có:

+ \(\widehat {MIN}\) là góc nội tiếp chắn cung \(AB\) nên $\widehat{MIN}=\frac{1}{2}sđ\overset\frown{AB}=30{}^\circ $

d) Xét đường tròn \(\left( I \right)\) có:

+ \(\widehat {MIN}\) là góc ở tâm chắn cung \(MN\) nên $\widehat{MIN}=sđ\overset\frown{MN}=30{}^\circ $

+ $sđ\overset\frown{M{{N}_{lớn}}}=360{}^\circ -sđ\overset\frown{M{{N}_{nhỏ}}}=360{}^\circ -30{}^\circ =330{}^\circ $

e) Xét đường tròn \(\left( I \right)\) có:

+ \(\widehat {MKN}\) là góc nội tiếp chắn cung \(MN\) nên $\widehat{MKN}=\frac{1}{2}sđ\overset\frown{MN}=15{}^\circ $

(Trả lời bởi datcoder)

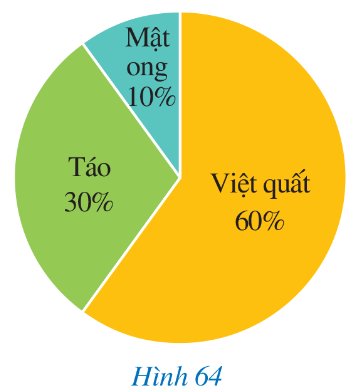
Hướng dẫn giải

- Do thành phần việt quất chiếm 60% số lượng học sinh.

Vì thế, cung tương ứng với phần biểu diễn thành phần việt quất là: \(\frac{{60}}{{100}}.360^\circ  = 216^\circ \).

- Do thành phần táo chiếm 30% số lượng học sinh.

Vì thế, cung tương ứng với phần biểu diễn thành phần táo là: \(\frac{{30}}{{100}}.360^\circ  = 108^\circ \).

- Do thành phần mật ong chiếm 10% số lượng học sinh.

Vì thế, cung tương ứng với phần biểu diễn thành phần mật ong là: \(\frac{{10}}{{100}}.360^\circ  = 36^\circ \). 

(Trả lời bởi datcoder)

Hướng dẫn giải

Xét đường tròn \(\left( I \right)\) có: \(\widehat {ABD}\) là góc nội tiếp chắn nửa đường tròn.

Vậy \(\widehat {ABD} = 90^\circ \).

Xét đường tròn \(\left( O \right)\) có: \(\widehat {ABC}\) là góc nội tiếp chắn nửa đường tròn.

Vậy \(\widehat {ABC} = 90^\circ \).

Ta có: \(\widehat {ABD} + \widehat {ABC} = 90^\circ  + 90^\circ  \Rightarrow \widehat {BDC} = 180^\circ \).

Vậy ba điểm \(B,D,C\) thẳng hàng.

(Trả lời bởi datcoder)

Hướng dẫn giải

Bước 1. Vẽ đường tròn tâm O, kẻ đường kính BC.

Bước 2. Lấy điểm A thuộc đường tròn (O) (A khác B, C). Ta được tam giác ABC vuông tại A.

Thật vậy, xét đường tròn (O) có đường kính BC, điểm A thuộc (O) nên \(\widehat{BAC}=90^o\) (góc nội tiếp chắn nửa đường tròn).

Vậy tam giác ABC vuông tại A.

(Trả lời bởi datcoder)