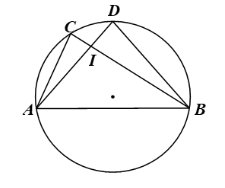
Ta có: \(\widehat {ACB}\) và \(\widehat {ADB}\) là hai góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \widehat {ADB}\) hay \(\widehat {ACI} = \widehat {BDI}\).
Do \(\widehat {CIA}\) và \(\widehat {DIB}\) là hai góc đối đỉnh nên \(\widehat {CIA} = \widehat {DIB}\).
Xét \(\Delta CIA\) và \(\Delta DIB\) có:
$\left\{ \begin{align}\widehat{ACI}=\widehat{BDI} \\ \widehat{CIA}=\widehat{DIB} \end{align} \right.\Rightarrow \Delta CIA\backsim \Delta DIB\left( g.g \right) \Rightarrow \frac{CI}{DI}=\frac{IA}{IB}\Rightarrow IA.ID=IC.IB.$
Đúng 0
Bình luận (0)



