Bài 3. Góc ở tâm, góc nội tiếp

Hướng dẫn giải

Gọi H là tiếp điểm của tiếp tuyến của đường tròn đã cho.

Xét tam giác OHB vuông tại H, ta có:

cos\(\widehat {HOB}\)= \(\frac{{OH}}{{OB}} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2}\)

suy ra \(\widehat {HOB}\) = 30^o

Ta có OA = OB (= R) nên tam giác OAB cân tại O

Mà OH là đường cao của tam giác AOB

Nên OH cũng là đường phân giác của tam giác AOB

Suy ra \(\widehat {AOB} = 2\widehat {HOB} = {2.30^o} = {60^o}\)

Do đó sđ\(\overset\frown{AB}\) =\(\widehat {AOB} = {60^o}\).

(Trả lời bởi datcoder)

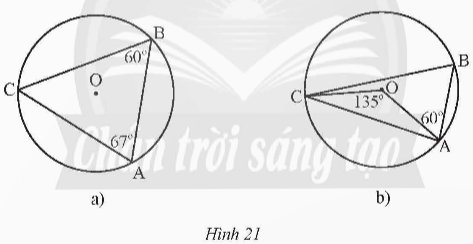
Hướng dẫn giải

a) Xét tam giác ABC, ta có: \(\widehat{ACB}={{180}^{o}}-\widehat{CBA}-\widehat{BAC}={{180}^{o}}-{{60}^{o}}-{{67}^{o}}={{53}^{o}}\)

Ta có sđ\(\overset\frown{AB}\) = 2.\(\widehat{ACB}\) = 2. 53^o = 106^o (Vì \(\overset\frown{AB}\) và \(\widehat{ACB}\) cùng chắn cung AB)

Ta có sđ\(\overset\frown{BC}\) = 2.\(\widehat{BAC}\) = 2. 67^o = 134^o (Vì \(\overset\frown{BC}\) và \(\widehat{BAC}\) cùng chắn cung BC)

Ta có sđ\(\overset\frown{AC}\) = 2.\(\widehat{ABC}\) = 2. 60^o = 120^o (Vì \(\overset\frown{AC}\) và \(\widehat{ABC}\) cùng chắn cung AC).

b) Ta có sđ\(\overset\frown{AC}\) và góc ở tâm \(\widehat{COA}\) cùng chắn cung AC

suy ra sđ\(\overset\frown{AC}\) = \(\widehat{COA}\) = 135^o.

Nối O với B.

Xét tam giác OAB có AO = OB (= R) suy ra tam giác OAB cân tại A.

Mặt khác, \(\widehat {OAB} = {60^o}\) nên tam giác OAB là tam giác đều.

Ta có sđ\(\overset\frown{AB}\) = \(\widehat{AOB}\) = \({{60}^{o}}\) (Vì \(\overset\frown{AB}\) và \(\widehat{AOB}\) cùng chắn cung AB)

Suy ra sđ\(\overset\frown{BC}\) = 360^o - sđ\(\overset\frown{AB}\) - sđ\(\overset\frown{AC}\) = 360^o - \({60^o}\) - 135^o = 165^o.

(Trả lời bởi datcoder)

Hướng dẫn giải

Ta có SM \( \bot \) OM (Tính chất tiếp tuyến)

Suy ra tam giác OSM vuông tại M

Ta có \(\widehat {MSO} + \widehat {MOS} = {90^o}\)

Và  AB\( \bot \)CD (gt)

Suy ra \(\widehat {MOS} + \widehat {MOA} = {90^o}\)

Nên \(\widehat {MSO} = \widehat {MOA}\) hay \(\widehat {MSD} = \widehat {MOA}\) (1)

Ta có \(\widehat {MOA} = 2\widehat {MBA}\) (góc ở tâm cùng chắn cung AM) (2)

Từ (1) và (2) suy ra \(\widehat {MSD} = 2\widehat {MBA}\).

(Trả lời bởi datcoder)