Chuyển số 44 ở hệ thập phân thành số ở hệ nhị phân bằng cách thực hiện theo hướng dẫn từng bước trong bảng sau:
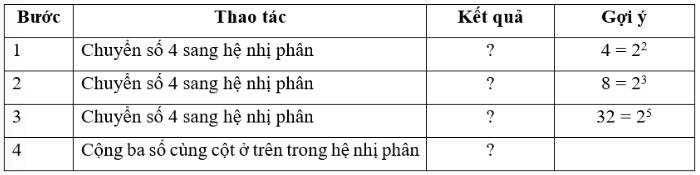
Chuyển số 44 ở hệ thập phân thành số ở hệ nhị phân bằng cách thực hiện theo hướng dẫn từng bước trong bảng sau:

Thực hiện phép cộng và phép nhân hai số nhị phân. Tạo bảng theo mẫu bên.
| x | |
| y | |
| x + y | |
| x * y |
Thảo luận (1)Hướng dẫn giải
Tính số bù của một số nhị phân
a) Cho số nhị phân x. Kết quả của phép toán NOT x kí hiệu là \(\overline{x}\). Ta gọi \(\overline{x}\) là số bù 1 của x. Em hãy viết số bù 1 của số 44 ở hệ nhị phân
b) Cho số nhị phân x. Kết quả của phép toán \(\overline{x}\)+1 gọi là số bù 2 của x. Em hãy viết số bù 2 của số 44 ở hệ nhị phân.
Thảo luận (1)Hướng dẫn giảia) Một số bù 1 có thể có được do đảo tất cả các bit có trong số nhị phân. Số 44 ở hệ nhị phân là: 101100, vậy số bù 1 của số 44 ở hệ nhị phân là: 010011.
b) Số bù 2 của số 44 ở hệ nhị phân: 010011 + 1= 010100.
(Trả lời bởi Toru)
Em hãy thực hiện phép cộng số nhị phân x có giá trị thập phân là 44 với số bù 2 của x và cho biết kết quả nếu quy ước độ dài dãy bit biểu diễn số nguyên trong máy là 1 byte.
Thảo luận (1)Hướng dẫn giải- Số nhị phân x có giá trị thập phân là 44: 00101100.
- Số bù 1 của số trên là: 11010011.
- Số bù 2 của số trên là: 11010011+ 1 = 11010100.
Tổng số nhị phân x và số bù 2 của nó là: 00101100 + 11010100 = 100000000.
(Trả lời bởi GV Nguyễn Trần Thành Đạt)
Một bài kiểm tra môn Tin học gồm 10 câu hỏi trắc nghiệm đúng – sai. Đáp án được biểu diễn bằng dãy 10 bit, kí hiệu là DapAn. Trả lời của thí sinh được biểu diễn bằng dãy 10 bit, kí hiệu là TraLoi.
- Em hãy dùng phép toán bit để tạo ra KetQua là dãy 10 bit, biểu diễn kết quả chấm từng câu hỏi, dúng là 1, sai là 0.
- Em hãy tính điểm cho thí sinh theo thang điểm 10.
Thảo luận (1)Hướng dẫn giảiTa sẽ gọi dãy bit DapAn là 0000000000 (10 số 0).
Dãy bit TraLoi của thí sinh sẽ gồm 10 bit toàn 0 và 1.
Phép cộng dãy bit TraLoi với DapAn sẽ cho ta dãy bit KetQua bởi vì: Nếu thí sinh trả lời đúng thì 1 + 0 = 1 (kết quả đúng), nếu thí sinh trả lời sai thì 0 + 0 = 0 (kết quả sai).
Điểm của thí sinh sẽ tính bằng số lượng bit có giá trị bằng 1 của KetQua.
Ví dụ: Thí sinh trả lời đúng câu 1, 2, 4, 5, 7, 9, 10.
Ta sẽ có dãy bit TraLoi là: 1101101011.
Và kết quả là:
1101101011
+
0000000000
= 1101101011
KetQua có 7 số 1 nên thí sinh được 7 điểm.
(Trả lời bởi Toru)