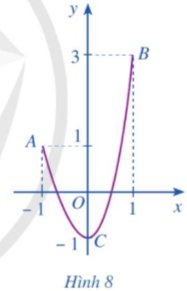
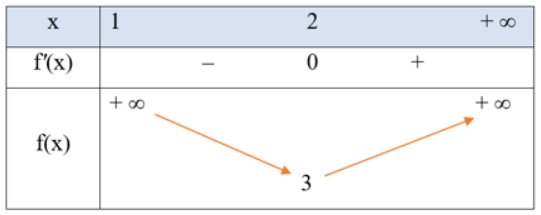
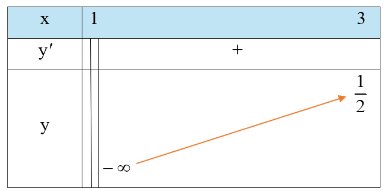
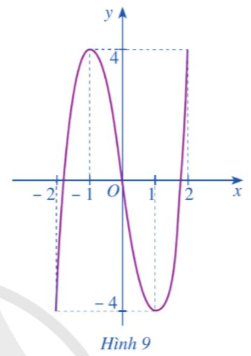
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
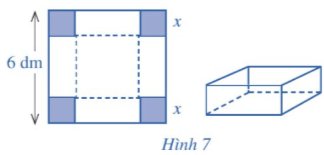
V được tính theo x bởi công thức nào? Có thể tìm giá trị lớn nhất của V bằng cách nào?