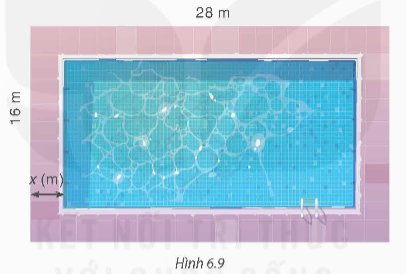
Trên một mảnh đất hình chữ nhật có kích thước 28 m × 16 m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là 288 m2?
Trên một mảnh đất hình chữ nhật có kích thước 28 m × 16 m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là 288 m2?

Xét bài toán trong tình huống mở đầu.
Gọi x (m) là bề rộng của mặt đường (0 < x < 8). Tính chiều dài và chiều rộng của bể bơi theo x.
Thảo luận (1)Hướng dẫn giảiChiều dài của bể bơi là: \(28 - 2x\left( m \right)\).
Chiều rộng của bể bơi là: \(16 - 2x\left( m \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
Dựa vào kết quả HĐ1, tính diện tích của bể bơi theo x.
Thảo luận (1)Hướng dẫn giảiDiện tích của bể bơi là: \(\left( {28 - 2x} \right)\left( {16 - 2x} \right) = 4{x^2} - 88x + 448\left( {{m^2}} \right)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Sử dụng giả thiết và kết quả HĐ2, hãy viết phương trình để tìm x.
Thảo luận (1)Hướng dẫn giảiVì diện tích của bể bơi là \(288{m^2}\) nên ta có phương trình:
\(\begin{array}{l}4{x^2} - 88x + 448 = 288\\4{x^2} - 88x + 160 = 0\end{array}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Trong các phương trình sau, những phương trình nào là phương trình bậc hai ẩn x? Chỉ rõ các hệ số a, b, c của mỗi phương trình đó.
a) x2 + 5 = 0;
b) 2x2 + 7x = 0;
c) \(\dfrac{x^2-2x+5}{x}=0\);
d) 0,5x2 = 0.
Thảo luận (1)Hướng dẫn giảia) Phương trình \({x^2} + 5 = 0\) là phương trình bậc hai với \(a = 1,b = 0,c = 5\).
b) Phương trình \(2{x^2} + 7x = 0\) là phương trình bậc hai với \(a = 2,b = 7,c = 0\).
c) Phương trình \(\frac{{{x^2} - 2x + 5}}{x} = 0\) không là phương trình bậc hai.
d) Phương trình \(0,5{x^2} = 0\) là phương trình bậc hai với \(a = 0,5,b = 0,c = 0\).
(Trả lời bởi Nguyễn Quốc Đạt)
Anh Pi nói rằng: “Phương trình (ẩn x) mx2 + 2x + 1 = 0 (m là một số cho trước) là một phương trình bậc hai với a = m, b = 2, c = 1”.
Ý kiến của em thế nào?
Thảo luận (1)Hướng dẫn giảiVới \(m = 0\) thì phương trình đã cho trở thành: \(2x + 1 = 0\), đây không phải là phương trình bậc hai.
Vậy ý kiến của Pi là sai.
(Trả lời bởi Nguyễn Quốc Đạt)
Giải các phương trình sau:
a) 2x2 + 6x = 0;
b) 5x2 + 11x = 0.
Thảo luận (1)Hướng dẫn giảia) \(2{x^2} + 6x = 0\)
\(2x\left( {x + 3} \right) = 0\)
\(x = 0\) hoặc \(x = - 3\)
Vậy phương trình có hai nghiệm \(x = 0\); \(x = - 3\).
b) \(5{x^2} + 11x = 0\)
\(x\left( {5x + 11} \right) = 0\)
\(x = 0\) hoặc \(x = - \frac{{11}}{5}\)
Vậy phương trình có hai nghiệm \(x = 0\); \(x = - \frac{{11}}{5}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Giải các phương trình sau:
a) x2 – 25 = 0;
b) (x + 3)2 = 5.
Thảo luận (1)Hướng dẫn giảia) \({x^2} - 25 = 0\)
\({x^2} = 25\)
\(x = 5\) hoặc \(x = - 5\)
Vậy phương trình có hai nghiệm \(x = 5\); \(x = - 5\).
b) \({\left( {x + 3} \right)^2} = 5\)
\(x + 3 = \sqrt 5 \) hoặc \(x + 3 = - \sqrt 5 \)
\(x = - 3 + \sqrt 5 \) hoặc \(x = - 3 - \sqrt 5 \)
Vậy phương trình có hai nghiệm \(x = - 3 + \sqrt 5 \); \(x = - 3 - \sqrt 5 \).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho phương trình x2 + 6x = 1.
Hãy cộng vào cả hai vế của phương trình với cùng một số thích hợp để được một phương trình mà vế trái có thể biến đổi thành một bình phương. Từ đó, hãy giải phương trình đã cho.
Thảo luận (1)Hướng dẫn giải\({x^2} + 6x = 1\)
\({x^2} + 2.x.3 + {3^2} = 1 + 9\)
\({\left( {x + 3} \right)^2} = 10\)
\(x + 3 = \sqrt {10} \) hoặc \(x + 3 = - \sqrt {10} \)
\(x = - 3 + \sqrt {10} \) \(x = - 3 - \sqrt {10} \)
Vậy phương trình có hai nghiệm \(x = - 3 + \sqrt {10} \); \(x = - 3 - \sqrt {10} \).
(Trả lời bởi Nguyễn Quốc Đạt)
Thực hiện lần lượt các bước sau để giải phương trình:
2x2 – 8x + 3 = 0.
a) Chuyển hạng tử tự do sang vế phải.
b) Chia cả hai vế của phương trình cho hệ số của x2.
c) Thêm vào hai vế của phương trình nhận được ở câu b với cùng một số để vế trái có thể biến đổi thành một bình phương. Từ đó tìm nghiệm x.
Thảo luận (1)Hướng dẫn giảia) Chuyển hạng tử tự do của phương trình sang vế phải ta được phương trình \(2{x^2} - 8x = - 3\).
b) Chia cả hai vế của phương trình cho hệ số của \({x^2}\) ta được: \({x^2} - 4x = \frac{{ - 3}}{2}\).
c) \({x^2} - 4x = \frac{{ - 3}}{2}\)
\({x^2} - 4x + 4 = \frac{{ - 3}}{2} + 4\)
\({\left( {x - 2} \right)^2} = \frac{5}{2}\)
\(x - 2 = \frac{{\sqrt {10} }}{2}\) hoặc \(x - 2 = - \frac{{\sqrt {10} }}{2}\)
\(x = 2 + \frac{{\sqrt {10} }}{2}\) \(x = 2 - \frac{{\sqrt {10} }}{2}\)
Vậy phương trình có hai nghiệm \(x = 2 + \frac{{\sqrt {10} }}{2}\); \(x = 2 - \frac{{\sqrt {10} }}{2}\).
(Trả lời bởi Nguyễn Quốc Đạt)