Trong không gian Oxyz, mắt một người quan sát ở điểm M(2; 3; −4) và vật cần quan sát đặt tại điểm N(−1; 0; 8). Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm O(0; 0; 0), bán kính bằng 3 và đặt trong mặt phẳng Oxy. Hỏi tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm N hay không?
Bài 15. Phương trình đường thẳng trong không gian
Mở đầu (SGK Kết nối tri thức với cuộc sống - Trang 41)
Thảo luận (0)
Hoạt động 1 (SGK Kết nối tri thức với cuộc sống - Trang 41)
Trong không gian, cho điểm M và vectơ \(\overrightarrow{u}\) khác vectơ – không. Khẳng định nào trong hai khẳng định sau là đúng?
a) Có duy nhất đường thẳng đi qua M và vuông góc với giá của \(\overrightarrow{u}\).
b) Có duy nhất đường thẳng đi qua M và song song hoặc trùng với giá của \(\overrightarrow{u}\).
Thảo luận (1)Hướng dẫn giảiKhẳng định đúng: Có duy nhất đường thẳng đi qua M và song song hoặc trùng với giá của \(\overrightarrow u \).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 1 (SGK Kết nối tri thức với cuộc sống - Trang 42)
Cho hình lăng trụ ABC.A'B'C' (H.5.25). Trong các vectơ có điểm đầu và điểm cuối đều là đỉnh của hình lăng trụ, những vectơ nào là vectơ chỉ phương của đường thẳng AB?
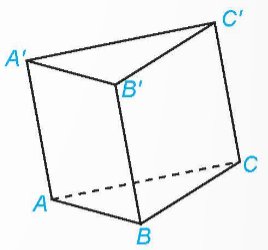
Thảo luận (1)Hướng dẫn giảiĐường thẳng AB nhận các vectơ \(\overrightarrow {AB} ,\overrightarrow {A'B'},\overrightarrow {B'A'} ,\overrightarrow {BA} \) là các vectơ chỉ phương.
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 2 (SGK Kết nối tri thức với cuộc sống - Trang 42)
Trong không gian Oxyz, một vật thể chuyển động với vectơ vận tốc không đổi overrightarrow{u} (a; b; c) ≠ overrightarrow{0} và xuất phát từ điểm A(x0; y0; z0) (H.5.26).a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm mà nó đi qua và vectơ chỉ phương của đường thẳng đó)?b) Giả sử tại thời điểm t (t 0) tính từ khi xuất phát, vật thể ở vị trí M(x; y; z). Tính x, y, z theo a, b, c, x0, y0, z0 và t.
Đọc tiếp
Trong không gian Oxyz, một vật thể chuyển động với vectơ vận tốc không đổi \(\overrightarrow{u}\)= (a; b; c) ≠ \(\overrightarrow{0}\) và xuất phát từ điểm A(x0; y0; z0) (H.5.26).
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm mà nó đi qua và vectơ chỉ phương của đường thẳng đó)?
b) Giả sử tại thời điểm t (t > 0) tính từ khi xuất phát, vật thể ở vị trí M(x; y; z). Tính x, y, z theo a, b, c, x0, y0, z0 và t.
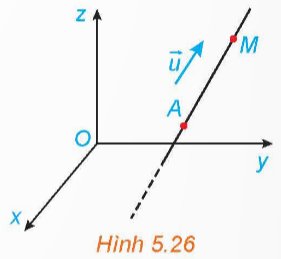
Thảo luận (1)Hướng dẫn giảia) Vật chuyển động trên đường thẳng qua A và song song với giá của vectơ \(\overrightarrow u \) (đi qua điểm A và vectơ chỉ phương của đường thẳng là \(\overrightarrow u \)).
b) Tại thời điểm t, vật ở vị trí \(M\left( {x;{\rm{ }}y;{\rm{ }}z} \right)\) nên: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 2 (SGK Kết nối tri thức với cuộc sống - Trang 43)
Trong không gian Oxyz, cho đường thẳng \(\Delta:\left\{{}\begin{matrix}x=2+t\\y=3t\\z=1+t\end{matrix}\right.\).
a) Hãy chỉ ra hai điểm thuộc ∆ và một vectơ chỉ phương của ∆.
b) Viết phương trình tham số của đường thẳng đi qua gốc tọa độ O(0; 0; 0) và có vectơ chỉ phương \(\overrightarrow{v}=\left(1;3;1\right)\).
Thảo luận (1)Hướng dẫn giảia) Vì \(\Delta \) có phương trình \(\left\{ \begin{array}{l}x = 2 + t\\y = 3t\\z = 1 + t\end{array} \right.\) nên điểm \(M\left( {2;0;1} \right)\) và điểm \(N\left( {3;3;2} \right)\) thuộc \(\Delta \) và \(\overrightarrow u \left( {1;3;1} \right)\) là một vectơ chỉ phương của \(\Delta \).
b) Phương trình tham số của đường thẳng đi qua gốc tọa độ \(O\left( {0;0;0} \right)\) và có vectơ chỉ phương \(\overrightarrow v = \left( {1;3;1} \right)\) là: \(\left\{ \begin{array}{l}x = t\\y = 3t\\z = t\end{array} \right.\)
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 3 (SGK Kết nối tri thức với cuộc sống - Trang 43)
Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm A(x0; y0; z0) và có vectơ chỉ phương overrightarrow{u} (a; b; c) (a, b, c là các số khác 0).a) Điểm M(x; y; z) thuộc ∆ khi và chỉ khi hai vectơ overrightarrow{AM}left(x-x_0;y-y_0;z-z_0right) và overrightarrow{u}left(a;b;cright) có mối quan hệ gì?b) Điểm M(x; y; z) thuộc ∆ khi và chỉ khi các số dfrac{x-x_0}{a},dfrac{y-y_0}{b},dfrac{z-z_0}{c} có mối quan hệ gì?
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm A(x0; y0; z0) và có vectơ chỉ phương \(\overrightarrow{u}\) = (a; b; c) (a, b, c là các số khác 0).
a) Điểm M(x; y; z) thuộc ∆ khi và chỉ khi hai vectơ \(\overrightarrow{AM}=\left(x-x_0;y-y_0;z-z_0\right)\) và \(\overrightarrow{u}=\left(a;b;c\right)\) có mối quan hệ gì?
b) Điểm M(x; y; z) thuộc ∆ khi và chỉ khi các số \(\dfrac{x-x_0}{a},\dfrac{y-y_0}{b},\dfrac{z-z_0}{c}\) có mối quan hệ gì?
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow {AM} \) cùng phương với \(\overrightarrow u \)
b) Chúng bằng nhau
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 3 (SGK Kết nối tri thức với cuộc sống - Trang 43)
Trong không gian Oxyz, cho đường thẳng \(\Delta:\dfrac{x+1}{3}=\dfrac{y-1}{1}=\dfrac{z-2}{5}\). Hãy chỉ ra một vectơ chỉ phương của ∆ và hai điểm thuộc ∆.
Thảo luận (1)Hướng dẫn giảiVì \(\Delta \) có phương trình \(\frac{{x - \left( { - 1} \right)}}{3} = \frac{{y - 1}}{1} = \frac{{z - 2}}{5}\) nên điểm \(M\left( { - 1;1;2} \right)\) và điểm N(2; 2; 7) thuộc \(\Delta \) và \(\overrightarrow u \left( {3;1;5} \right)\) là một vectơ chỉ phương của \(\Delta \).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 4 (SGK Kết nối tri thức với cuộc sống - Trang 44)
Trong không gian Oxyz, viết phương trình tham số và phương trình chính tắc của đường thẳng ∆ đi qua điểm A(2; −1; 0) và có vectơ chỉ phương \(\overrightarrow{u}\) = (−1; 2; 3).
Thảo luận (1)Hướng dẫn giảiĐường thẳng \(\Delta \) có phương trình tham số là: \(\left\{ \begin{array}{l}x = 2 - t\\y = - 1 + 2t\\z = 3t\end{array} \right.\) và phương trình chính tắc là:
\(\frac{{x - 2}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{z}{3}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 5 (SGK Kết nối tri thức với cuộc sống - Trang 44)
Trong không gian Oxyz, viết phương trình tham số của đường thẳng ∆ đi qua điểm M(2; −1; 3) và vuông góc với mặt phẳng Oyz.
Thảo luận (1)Hướng dẫn giảiMặt phẳng (Oyz) có một vectơ pháp tuyến là \(\overrightarrow i = \left( {1;0;0} \right)\).
Vì đường thẳng \(\Delta \) vuông góc với mặt phẳng (Oyz) nên đường thẳng \(\Delta \) nhận \(\overrightarrow i = \left( {1;0;0} \right)\) làm một vectơ chỉ phương. Phương trình tham số của \(\Delta \): \(\left\{ \begin{array}{l}x = 2 + t\\y = - 1\\z = 3\end{array} \right.\)
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 4 (SGK Kết nối tri thức với cuộc sống - Trang 44)
Trong không gian Oxyz, cho hai điểm phân biệt A1(x1; y1; z1), A2(x2; y2; z2).
a) Hãy chỉ ra một vectơ chỉ phương của đường thẳng A1A2.
b) Viết phương trình đường thẳng A1A2.
Thảo luận (1)Hướng dẫn giảia) Một vectơ chỉ phương của đường thẳng \({A_1}{A_2}\) là \(\overrightarrow {{A_1}{A_2}} \).
b) Đường thẳng \({A_1}{A_2}\) có vectơ chỉ phương là \(\overrightarrow {{A_1}{A_2}} \left( {{x_2} - {x_1};{y_2} - {y_1};{z_2} - {z_1}} \right)\).
Mà đường thẳng \({A_1}{A_2}\) đi qua điểm \({A_1}\left( {{x_1};{y_1};{z_1}} \right)\) nên phương trình đường thẳng tham số \({A_1}{A_2}\) là: \(\left\{ \begin{array}{l}x = {x_1} + \left( {{x_2} - {x_1}} \right)t\\y = {y_1} + \left( {{y_2} - {y_1}} \right)t\\z = {z_1} + \left( {{z_2} - {z_1}} \right)t\end{array} \right.\)
Phương trình chính tắc của đường thẳng \({A_1}{A_2}\) là: \(\frac{{x - {x_1}}}{{{x_2} - {x_1}}} = \frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{z - {z_1}}}{{{z_2} - {z_1}}}\).
(Trả lời bởi Nguyễn Quốc Đạt)