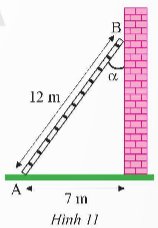
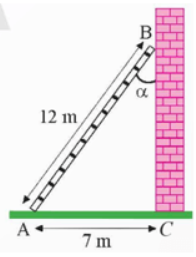
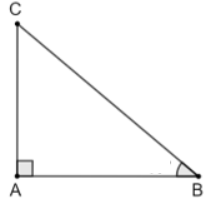
a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):
22o; 52o; 15o20’; 52o18’
b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút):
sin x = 0,723 cos y = 0,828 tan z = 3,77 cot t = 1,54.