Cho hai điểm M(2; 1; 0) và N(0; 3; 0). Lập phương trình mặt phẳng trung trực của đoạn thẳng MN.
Bài 1: Phương trình mặt phẳng
Luyện tập 5 (SGK Cánh Diều - Tập 2 - Trang 54)
Thảo luận (1)
Hoạt động 6 (SGK Cánh Diều - Tập 2 - Trang 55)
Cho mặt phẳng (P) đi qua điểm I(1; 3; – 2) có cặp vectơ chỉ phương là overrightarrow{u}left(1;1;3right),overrightarrow{v}left(2;-1;2right) (Hình 10).a) Hãy chỉ ra một vectơ pháp tuyến overrightarrow{n} của mặt phẳng (P).b) Lập phương trình mặt phẳng (P) đi qua điểm I(1; 3; – 2), biết vectơ pháp tuyến overrightarrow{n}.
Đọc tiếp
Cho mặt phẳng (P) đi qua điểm I(1; 3; – 2) có cặp vectơ chỉ phương là \(\overrightarrow{u}=\left(1;1;3\right),\overrightarrow{v}=\left(2;-1;2\right)\) (Hình 10).
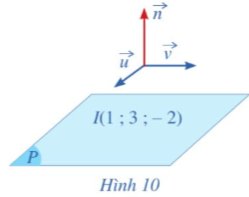
a) Hãy chỉ ra một vectơ pháp tuyến \(\overrightarrow{n}\) của mặt phẳng (P).
b) Lập phương trình mặt phẳng (P) đi qua điểm I(1; 3; – 2), biết vectơ pháp tuyến \(\overrightarrow{n}\).
Thảo luận (1)Hướng dẫn giảia) Vecto pháp tuyến của mặt phẳng (P) là:
\(\overrightarrow n = [\overrightarrow u ;\overrightarrow v ] = (5; - 4;3)\).
b) Phương trình mặt phẳng (P):
\(5(x - 1) - 4(y - 3) + 3(z + 2) = 0 \)
\(\Leftrightarrow 5x - 4y + 3z + 13 = 0\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 6 (SGK Cánh Diều - Tập 2 - Trang 55)
Cho mặt phẳng (P) đi qua điểm I(x0; y0; z0). Lập phương trình mặt phẳng (P), biết mặt phẳng đó có cặp vectơ chỉ phương là \(\overrightarrow{i},\overrightarrow{j}\).
Thảo luận (1)Hướng dẫn giảiCặp vecto chỉ phương \(\overrightarrow i \), \(\overrightarrow j \) của (P) đều thuộc mặt phẳng (Oxy). Do đó, vecto pháp tuyến của (P) vuông góc với mặt phẳng (Oxy). Ta lấy \(\overrightarrow k = (0;0;1)\) thỏa mãn điều kiện trên.
Mặt phẳng (P) đi qua \(I\left( {{x_0};{y_0};{z_0}} \right)\), nhận \(\overrightarrow k = (0;0;1)\) làm vecto pháp tuyến có phương trình:
\(0\left( {x - {x_0}} \right) + 0\left( {y - {y_0}} \right) + 1\left( {z - {z_0}} \right) = 0 \Leftrightarrow z - {z_0} = 0\).
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 7 (SGK Cánh Diều - Tập 2 - Trang 55)
Cho ba điểm H(– 1; 1; 2), I(1; 3; 2), K(– 1; 4; 5) cùng thuộc mặt phẳng (P) (Hình 11).a) Tìm tọa độ của các vectơ overrightarrow{HI},overrightarrow{HK}. Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng.b) Lập phương trình mặt phẳng (P) đi qua điểm H(– 1; 1; 2), biết cặp vectơ chỉ phương là overrightarrow{HI},overrightarrow{HK}.
Đọc tiếp
Cho ba điểm H(– 1; 1; 2), I(1; 3; 2), K(– 1; 4; 5) cùng thuộc mặt phẳng (P) (Hình 11).

a) Tìm tọa độ của các vectơ \(\overrightarrow{HI},\overrightarrow{HK}\). Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng.
b) Lập phương trình mặt phẳng (P) đi qua điểm H(– 1; 1; 2), biết cặp vectơ chỉ phương là \(\overrightarrow{HI},\overrightarrow{HK}\).
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow {HI} = (2;2;0)\), \(\overrightarrow {HK} = (0;3;3)\).
Có \(\overrightarrow {HI} \ne k.\overrightarrow {HK} \) suy ra H, I, K không thẳng hàng.
b) Vecto pháp tuyến của mặt phẳng (P) là:
\(\overrightarrow n = [\overrightarrow {HI} ;\overrightarrow {HK} ] = (6; - 6;6)\).
Phương trình mặt phẳng (P) là:
\(6(x + 1) - 6(y - 1) + 6(z - 2) = 0 \)
\(\Leftrightarrow 6x - 6y + 6z = 0 \)
\(\Leftrightarrow x - y + z = 0\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 7 (SGK Cánh Diều - Tập 2 - Trang 56)
Lập phương trình mặt phẳng đi qua ba điểm M(1; 2; 1), N(0; 3; 2) và P(– 1; 0; 0).
Thảo luận (1)Hướng dẫn giảiTa có: \(\overrightarrow {MN} = ( - 1;1;1)\), \(\overrightarrow {MP} = ( - 2; - 2; - 1)\).
\(\overrightarrow n = \left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&1\\{ - 2}&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&{ - 1}\\{ - 1}&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&1\\{ - 2}&{ - 2}\end{array}} \right|} \right) = \left( {1; - 3;4} \right)\) là một vecto pháp tuyến của mặt phẳng cần tìm.
Phương trình mặt phẳng (MNP) là:
\(1(x - 1) - 3(y - 2) + 4(z - 1) = 0\)
\( \Leftrightarrow x - 3y + 4z - 1 = 0\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 8 (SGK Cánh Diều - Tập 2 - Trang 57)
Lập phương trình mặt phẳng đi qua ba điểm A(2; 0; 0), B(0; 3; 0), C(0; 0; 4).
Thảo luận (1)Hướng dẫn giảiPhương trình mặt phẳng (ABC) là:
\(\frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1\).
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 8 (SGK Cánh Diều - Tập 2 - Trang 57)
Cho mặt phẳng (P1): 2x + 2y + 2z + 1 0 (1)và mặt phẳng (P2): x + y + z – 1 0 (2)a) Gọi overrightarrow{n_1}left(2;2;2right),overrightarrow{n_2}left(1;1;1right) lần lượt là vectơ pháp tuyến của hai mặt phẳng (P1), (P2) (Hình 14). Tìm liên hệ giữa overrightarrow{n_1} và 2overrightarrow{n_2}.b) Tìm các hệ số tự do D1, D2 lần lượt trong hai phương trình (1), (2). So sánh D1 và 2D2.c) Nêu vị trí tương đối của hai mặt phẳng (P1), (P2).
Đọc tiếp
Cho mặt phẳng (P1):
2x + 2y + 2z + 1 = 0 (1)
và mặt phẳng (P2):
x + y + z – 1 = 0 (2)
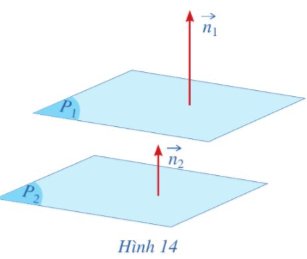
a) Gọi \(\overrightarrow{n_1}=\left(2;2;2\right),\overrightarrow{n_2}=\left(1;1;1\right)\) lần lượt là vectơ pháp tuyến của hai mặt phẳng (P1), (P2) (Hình 14). Tìm liên hệ giữa \(\overrightarrow{n_1}\) và \(2\overrightarrow{n_2}\).
b) Tìm các hệ số tự do D1, D2 lần lượt trong hai phương trình (1), (2). So sánh D1 và 2D2.
c) Nêu vị trí tương đối của hai mặt phẳng (P1), (P2).
Thảo luận (1)Hướng dẫn giảia) \(\overrightarrow {{n_1}} = 2\overrightarrow {{n_2}} = (2;2;2)\).
b) \({D_1}= 1\); \(2{D_2}= -2\).
Vậy \({D_1} \ne 2{D_2}\).
c) \(({P_1})//({P_2})\).
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 9 (SGK Cánh Diều - Tập 2 - Trang 58)
Cho m ≠ 0. Chứng minh rằng các mặt phẳng (P): x – m = 0, (Q): y – m = 0, (R): z – m = 0 lần lượt song song với các mặt phẳng (Oyz), (Ozx), (Oxy).
Thảo luận (1)Hướng dẫn giảiVecto pháp tuyến của các mặt phẳng (P), (Q), (R) là:
\(\overrightarrow {{n_P}} = (1;0;0)\), \(\overrightarrow {{n_Q}} = (0;1;0)\), \(\overrightarrow {{n_R}} = (0;0;1)\).
Vecto pháp tuyến của các mặt phẳng (Oyz): x = 0, (Ozx): y = 0, (Oxy): z = 0 là:
\(\overrightarrow i = (1;0;0)\), \(\overrightarrow j = (0;1;0)\), \(\overrightarrow k = (0;0;1)\).
Do \(\overrightarrow i = \overrightarrow {{n_P}} \) và \(m \ne 0\) nên (P) // (Oyz).
Do \(\overrightarrow j = \overrightarrow {{n_Q}} \) và \(m \ne 0\) nên (Q) // (Ozx).
Do \(\overrightarrow k = \overrightarrow {{n_R}} \) và \(m \ne 0\) nên (R) // (Oxy).
(Trả lời bởi Nguyễn Quốc Đạt)
Hoạt động 9 (SGK Cánh Diều - Tập 2 - Trang 58)
Cho mặt phẳng (P1) có phương trình tổng quát là:x + 2y + z + 1 0và mặt phẳng (P2) có phương trình tổng quát là:3x – 2y + z + 5 0.Gọi overrightarrow{n_1}left(1;2;1right),overrightarrow{n_2}left(3;-2;1right) lần lượt là vectơ pháp tuyến của hai mặt phẳng (P1), (P2). Hai vectơ overrightarrow{n_1},overrightarrow{n_2} có vuông góc với nhau hay không?
Đọc tiếp
Cho mặt phẳng (P1) có phương trình tổng quát là:
x + 2y + z + 1 = 0
và mặt phẳng (P2) có phương trình tổng quát là:
3x – 2y + z + 5 = 0.
Gọi \(\overrightarrow{n_1}=\left(1;2;1\right),\overrightarrow{n_2}=\left(3;-2;1\right)\) lần lượt là vectơ pháp tuyến của hai mặt phẳng (P1), (P2). Hai vectơ \(\overrightarrow{n_1},\overrightarrow{n_2}\) có vuông góc với nhau hay không?

Thảo luận (1)Hướng dẫn giải\(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.3 + 2.( - 2) + 1.1 = 0\) suy ra \(\overrightarrow {{n_1}} \),\(\overrightarrow {{n_2}} \) vuông góc với nhau.
(Trả lời bởi Nguyễn Quốc Đạt)
Luyện tập 10 (SGK Cánh Diều - Tập 2 - Trang 59)
Chứng minh rằng hai mặt phẳng (Ozx) và (P): x + 2z – 3 = 0 vuông góc với nhau.
Thảo luận (1)Hướng dẫn giảiVecto pháp tuyến của mặt phẳng (Ozx) là \(\overrightarrow j = (0;1;0)\).
Vecto pháp tuyến của mặt phẳng (P) là \(\overrightarrow n = (1;0;2)\).
Ta có \(\overrightarrow j .\overrightarrow n = (0.1 + 1.0 + 0.2) = 0\) nên \(\overrightarrow j \bot \overrightarrow n \).
Vậy \((Ozx) \bot (P)\).
(Trả lời bởi Nguyễn Quốc Đạt)