Đổi số đo của các góc sau đây sang độ:
a) \(\frac{\pi }{{12}}\)
b) -5
c) \(\frac{{13\pi }}{9}\)
Bài 1. Góc lượng giác Toán
Bài tập 2 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Thảo luận (1)
Bài tập 3 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
a) \(\frac{{ - 17\pi }}{3}\)
b) \(\frac{{13\pi }}{4}\)
c) \( - 765^\circ \)
Thảo luận (1)Hướng dẫn giải
Bài tập 4 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Góc lượng giác \(\frac{{31\pi }}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
\(\frac{{3\pi }}{7};\,\,\frac{{10\pi }}{7};\,\,\frac{{ - 25\pi }}{7}\)
Thảo luận (1)Hướng dẫn giải\(\dfrac{31\pi}{7}=\dfrac{3\pi}{7}+2\cdot2\pi\\ -\dfrac{25\pi}{7}=-\dfrac{4\pi}{7}-3\pi\\ \dfrac{10\pi}{7}=\dfrac{3\pi}{7}+\pi\)
\(\Rightarrow\dfrac{31\pi}{7}\) có cùng biểu diễn trên đường tròn lượng giác với góc \(\dfrac{3\pi}{7}\)
(Trả lời bởi Hà Quang Minh)
Bài tập 5 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Viết công thức số đo tổng quát của các góc lượng giác (OA; OM) và \(\left( {OA;ON} \right)\) trong Hình 14:
Thảo luận (1)Hướng dẫn giảiTa có: \(\left(OA,OM\right)=120^o+k\cdot360^o,k\in Z\\ \left(OA,ON\right)=-75^o+k\cdot360^o,k\in Z\)
(Trả lời bởi Hà Quang Minh)
Bài tập 6 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).
Thảo luận (1)Hướng dẫn giảiVì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên mỗi phần có số đo bằng \(\dfrac{360^o}{5}=72^o\)
Ta có: \(\left(ON,OM\right)=\left(ON,Ox\right)+\left(Ox,OM\right)\\ \Rightarrow\left(ON,Ox\right)=99^o\)
Công thức số đo tổng quát của góc lượng giác \(\left(ON,Ox\right)=99^o+k\cdot360^o,k\in Z\)
(Trả lời bởi Hà Quang Minh)
Bài tập 7 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:
a) \(\frac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)
b) \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\)
Thảo luận (1)Hướng dẫn giải
Bài tập 8 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?frac{pi }{2} + kfrac{{2pi }}{3},,left( {k in mathbb{Z}} right);frac{{ - pi }}{6} + kfrac{{2pi }}{3},,left( {k in mathbb{Z}} right);frac{pi }{2} + kfrac{pi }{3},,left( {k in mathbb{Z}} right)
Đọc tiếp
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
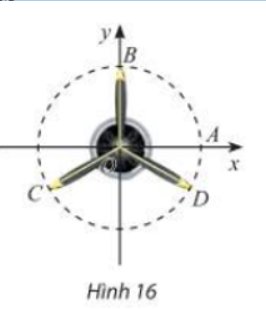
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Thảo luận (1)Hướng dẫn giải+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{{2\pi }}{3}\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 2 thì \(\frac{\pi }{2} + 2.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
+ Xét góc lượng giác \(\frac{\pi }{2} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 0 thì \(\frac{\pi }{2} + 0.\frac{{\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 1 thì \(\frac{\pi }{2} + 1.\frac{{\pi }}{3} =\frac{5\pi }{6} \) không biểu diễn bởi điểm nào.
+ Xét góc lượng giác \(\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\)
Với k = 1 thì \(\frac{{ - \pi }}{6}+ 1.\frac{{2\pi }}{3} =\frac{\pi }{2} \) được biểu diễn bởi điểm B.
Với k = 2 thì \(\frac{{ - \pi }}{6}+ 2.\frac{{2\pi }}{3} =\frac{7\pi }{6} \) được biểu diễn bởi điểm C.
Với k = 3 thì \(\frac{{ - \pi }}{6} + 3.\frac{{2\pi }}{3} =\frac{11\pi }{6} \) được biểu diễn bởi điểm D.
Vậy các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác
\(\frac{\pi }{2} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right);\frac{{ - \pi }}{6} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)\,\,\left( {k \in \mathbb{Z}} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Bài tập 9 (trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo)
Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc \(\alpha = {\left( {\frac{1}{{60}}} \right)^\circ }\) của đường kinh tuyến (Hình 17). Đổi số đo \(\alpha \) sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilomet, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.
Thảo luận (1)Hướng dẫn giảiTa có: \(\alpha=\left(\dfrac{1}{60}\right)^o\Rightarrow\alpha=\dfrac{\left(\pi\cdot\dfrac{1}{60}\right)}{180}=\dfrac{\pi}{10800}\)
Vậy một hải lí có độ dài bằng:
\(l=\dfrac{\pi Rn^o}{180^o}=\dfrac{\pi\cdot6371\cdot\left(\dfrac{1}{60}\right)^o}{180^o}\approx1,85\left(km\right)\)
(Trả lời bởi Hà Quang Minh)