Bài 5:
a: Phương trình hoành độ giao điểm là:
\(x^2-2x-m^2-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot\left(-m^2-1\right)\)
\(=4+4m^2+4=4m^2+8>0\)
Vậy: (P) cắt (d) tại hai điểm phân biệt
b: Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-1\end{matrix}\right.\)
Theo đề, ta có: \(x_A^2+x_B^2=14\)
\(\Leftrightarrow4-2\left(-m^2-1\right)=14\)
\(\Leftrightarrow2m^2=8\)
hay \(m\in\left\{2;-2\right\}\)









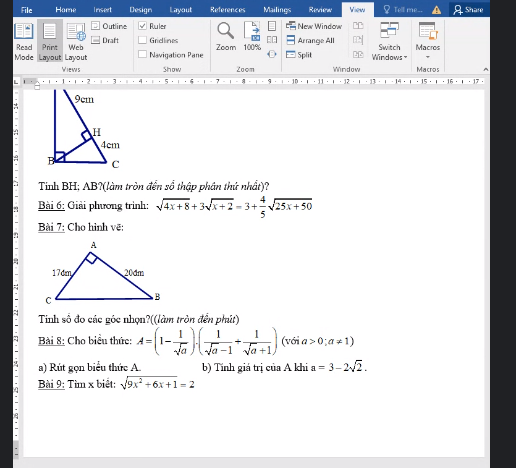 giúp em bài 8 với 9 ạ :<
giúp em bài 8 với 9 ạ :<


 giúp mình câu c bài 2
giúp mình câu c bài 2





