Bài 1:
a) Ta có: \(\left\{{}\begin{matrix}3x+2y=1\\x-y=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+2y=1\\3x-3y=-\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=\dfrac{5}{2}\\x-y=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{2}:5=\dfrac{5}{2}\cdot\dfrac{1}{5}=\dfrac{1}{2}\\x=-\dfrac{1}{2}+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{1}{2}=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
b) Ta có: \(\left\{{}\begin{matrix}3x-4y=11\\4x-3y=17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}12x-16y=44\\12x-9y=51\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7y=-7\\3x-4y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\3x=11+4\cdot y=11+4\cdot1=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)






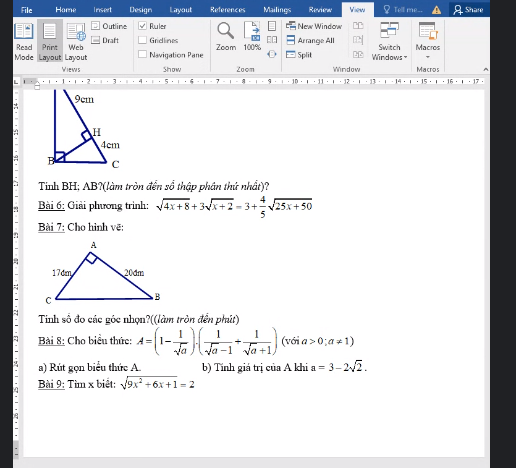 giúp em bài 8 với 9 ạ :<
giúp em bài 8 với 9 ạ :<









