Bài 4: Ôn tập chương Giới hạn
Các câu hỏi tương tự
Xét tính liên tục trên R của hàm số :
\(g\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^2-x-2}{x-2};\left(x>2\right)\\5-x;\left(x\le2\right)\end{matrix}\right.\)
Cho hàm số f(x) = \(\left\{{}\begin{matrix}x^2sin\dfrac{1}{x}\left(x\ne0\right)\\0\left(x=0\right)\end{matrix}\right.\)
a, Tính \(g\left(x\right)=\lim\limits_{t\rightarrow0}=\dfrac{f\left(x+t\right)-f\left(x-2t\right)}{2t}\) (x thuộc R)
b, Khảo sát sự tồn tại của g'(x) với x thuộc R
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
f(x) = \(\left\{{}\begin{matrix}\dfrac{2x^3-11x^2+17x-6}{x^2-x-6},x\ne3\\m^3-2m^2-3m+7,x=3\end{matrix}\right.\) liên tục tại x=3
Bài 1 :
Tìm các giá trị của m để hàm số \(f\left(x\right)=\left\{{}\begin{matrix}\frac{\sqrt{1-x}-\sqrt{1+x}}{x}khix< 0\\m+\frac{1-x}{1+x}khix\ge0\end{matrix}\right.\) liên tục tại x = 0 ?
Bài 2 : Chứng minh rằng phương trình \(4x^4+2x^2-x-3=0\) có ít nhất 2 nghiệm trong khoảng (-1;1)
Tìm tất cả các giá trị thực của m để hàm số \(f\left(x\right)=\left\{{}\begin{matrix}\frac{\sqrt{x+1}-1}{x}khix>0\\\sqrt{x^2+1}-mkhix\le0\end{matrix}\right.\) liên tục trên R
A. \(m=\frac{3}{2}\)
B. \(m=\frac{1}{2}\)
C. \(m=-2\)
D. \(m=-\frac{1}{2}\)
cho hàm số f(x) thoả mãn \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-2}{x-3}=\dfrac{1}{4}\)
tính \(I=\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-2}{\left(x-3\right)\left(\sqrt{5f\left(x\right)+6}+1\right)}\)
Giúp em với ạ em cảm ơn nhìu!!!!!
Giả sử hai hàm số yfleft(xright) và yfleft(x+dfrac{1}{2}right) đều liên tục trên đoạn left[0;1right] và fleft(0right)fleft(1right).
Chứng minh rằng phương trình fleft(xright)-fleft(x+dfrac{1}{2}right)0 luôn có nghiệm trong đoạn left[0;dfrac{1}{2}right] ?
Đọc tiếp
Giả sử hai hàm số \(y=f\left(x\right)\) và \(y=f\left(x+\dfrac{1}{2}\right)\) đều liên tục trên đoạn \(\left[0;1\right]\) và \(f\left(0\right)=f\left(1\right)\).
Chứng minh rằng phương trình \(f\left(x\right)-f\left(x+\dfrac{1}{2}\right)=0\) luôn có nghiệm trong đoạn \(\left[0;\dfrac{1}{2}\right]\) ?
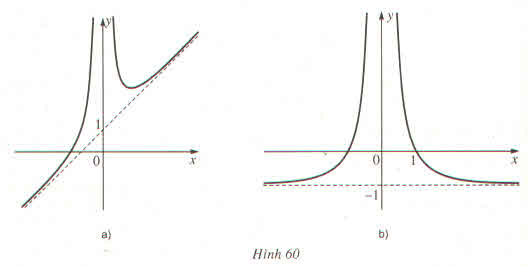
Cho hai hàm số fleft(xright)dfrac{1-x^2}{x^2} và gleft(xright)dfrac{x^3+x^2+1}{x^2}
a) Tính limlimits_{xrightarrow0}fleft(xright);limlimits_{xrightarrow0}gleft(xright);limlimits_{xrightarrow+infty}fleft(xright);limlimits_{xrightarrow+infty}gleft(xright)
b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường con nào là đồ thị của mỗi hàm số đó ?
Đọc tiếp
Cho hai hàm số \(f\left(x\right)=\dfrac{1-x^2}{x^2}\) và \(g\left(x\right)=\dfrac{x^3+x^2+1}{x^2}\)
a) Tính \(\lim\limits_{x\rightarrow0}f\left(x\right);\lim\limits_{x\rightarrow0}g\left(x\right);\lim\limits_{x\rightarrow+\infty}f\left(x\right);\lim\limits_{x\rightarrow+\infty}g\left(x\right)\)
b) Hai đường cong sau đây (h.60) là đồ thị của hai hàm số đã cho. Từ kết quả câu a), hãy xác định xem đường con nào là đồ thị của mỗi hàm số đó ?
Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}ax^2+bxkhix\ge1\\2x-1khix< 1\end{matrix}\right.\) .Để hàm số đã cho có đạo hàm tại x = 1 thì 2a + b bằng :
A. 2
B. 5
C. -2
D. -5






