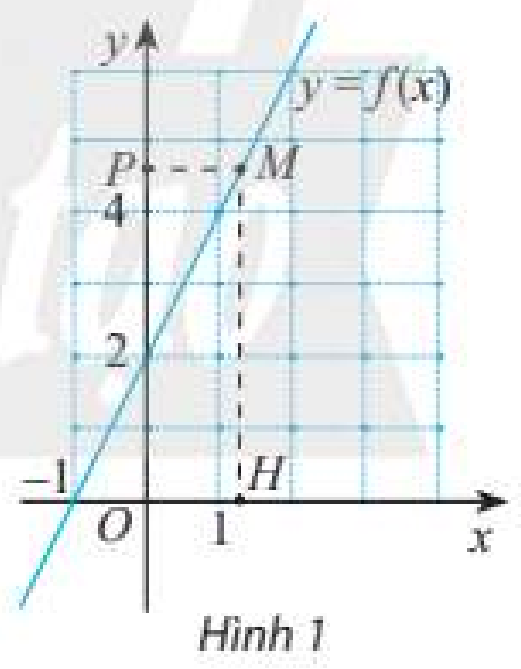
Giả sử điểm \(M\) có hoành độ là \(x\).
Độ dài \(OH\) là hoành độ của điểm \(M\). Vậy \(OH = x\).
Độ dài \(OK\) là tung độ của điểm \(M\). Vậy \(OK = \frac{1}{{{x^2}}}\).
\(S\left( x \right) = OH.OK = x.\frac{1}{{{x^2}}} = \frac{1}{x}\).
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty \). Vậy diện tích \(S\left( x \right)\) trở nên rất lớn khi \(x \to {0^ + }\).
\(\mathop {\lim }\limits_{x \to + \infty } S\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Vậy diện tích \(S\left( x \right)\) dần về 0 khi \(x \to + \infty \).