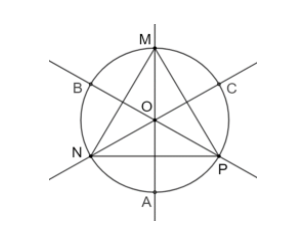
Gọi O là giao điểm của đường cao MA, NP và PC của tam giác MNP.
Ta có tam giác MNP đều nên MA, NB, PC là ba đường trung tuyến đồng thời là ba đường phân giác của tam giác.
Do đó, O là trọng tâm, đồng thời là tâm đường tròn nội tiếp tam giác MNP với bán kính r = OA = OB = OC.
Bán kính đường tròn ngoại tiếp tam giác là
r = \(\frac{{a\sqrt 3 }}{6} = \frac{{8\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{3}\) (cm).
Đúng 0
Bình luận (0)


