Question

Vẽ tam giác PQR có PQ = PR = 5cm, QR = 6cm. Lấy điểm M trên đường thẳng QR sao cho PM = 4,5 cm. Có mấy điểm M như vậy ? Điểm M có nằm trên cạnh QR hay không? Vì sao?

Answer 1

Kẻ đường cao AH của ∆PQR

=> H là trung điểm của QR

=> HR =\(\dfrac{1}{2}\) QR = 3cm

+ ∆PHR vuông tại H

nên PH² = PR² – HR² (định lý pytago)

PH² = 25- 9 = 16=> PH = 4cm

Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR. Vậy chắc chắn có một đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.

∆PHM vuông góc tại H nên HM² = PM² – PH² (định lý pytago)

=> HM² = 20,25 – 16 = 4, 25

=> HM = 2,1cm

Vậy trên đường thẳng QR có hai điểm M như vậy thỏa mãn điều kiện HM = 2,1cm

Vì HM < HR => M nằm giữa H và R hay hai điểm này nằm trên cạnh QR, và nằm khác phía đối với điểm H

Answer 2

Xét hai tam giác vuông tại H: ΔPHQ và ΔPHR có

PH chung

PQ = PR ( = 5cm)

⇒ ΔPHQ = ΔPHR (cạnh huyền – cạnh góc vuông)

⇒ HQ = HR (Hai cạnh tương ứng)

Mà HQ + HR = QR = 6 cm

+ ΔPHR vuông tại H có PR2= PH2+ HR2(định lí Py – ta – go)

⇒ PH2= PR2– HR2= 52– 32= 16 ⇒ PH = 4cm .

Đường vuông góc PH = 4cm là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.

Vậy chắc chắn có đường xiên PM = 4,5cm (vì PM = 4,5cm > 4cm) kẻ từ P đến đường thẳng QR.

+ Lại có : HM, HR lần lượt là hình chiếu của các đường xiên PM, PR trên đường thẳng QR.

Mà PM < PR ⇒ HM < HR = HQ (đường xiên nào lớn hơn thì hình chiếu lớn hơn).

⇒ M nằm giữa H và Q hoặc H và R

⇒ M nằm trên cạnh QP và có hai điểm M như vậy.

Answer 3

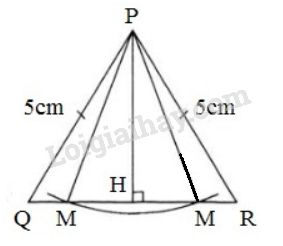
* Vẽ hình:

- Vẽ \(\Delta PQR\) có \(PQ=PR=5cm,QR=6cm.\)

+ Vẽ đoạn thẳng \(QR=6cm.\)

+ Vẽ cung tròn tâm và cung tròn tâm bán kính . Hai cung tròn này cắt nhau tại .

+ Nối \(PQ\) và \(PR\) ta được tam giác cần vẽ.

- Vẽ điểm : Vẽ cung tròn tâm bán kính cắt đường thẳng tại .

* Chứng minh:

Xét \(\Delta PQR\) có:

\(PQ=PR=5cm\left(gt\right)\)

=> \(\Delta PQR\) cân tại P.

Từ P kẻ đường thẳng \(PH\perp QR.\)

Gọi M là một điểm nằm trên đường thẳng \(QR.\)

Ta có: \(MH,QH,RH\) lần lượt là hình chiếu của \(PM,PQ,PR\) trên \(QR.\)

Vì \(PM< PQ=PR\) \(\left(4,5cm< 5cm\right).\)

=> \(\left\{{}\begin{matrix}MH< QH\\MH< RH\end{matrix}\right.\) (đường xiên nào lớn hơn thì có hình chiếu lớn hơn).

- Trên đoạn thẳng \(QH\) có:

\(MH< QH\left(cmt\right)\)

=> M nằm giữa 2 điểm Q và H.
- Trên đoạn thẳng \(RH\) có: \(MH< RH\left(cmt\right)\) => M nằm giữa 2 điểm R và H. => Có 2 điểm M thỏa mãn điều kiện đề bài và điểm này nằm trên cạnh .
Chúc bạn học tốt!