Chương 2: MẶT NÓN, MẶT TRỤ, MẶT CẦU
Các câu hỏi tương tự
Trong hệ trục Oxyz, cho hai mặt cầu (S1)left(x-1right)^2+left(y+3right)^2+left(z-2right)^249 và(S2) left(x-10right)^2+left(y-9right)^2+left(z-2right)^2400 và mặt phẳng (P) : 4x-3y+mz+220 . Có bao nhiêu sốnguyên m để mp (P) cắt hai mặt cầu (S1), (S2) theo giao tuyến là hai đường tròn không có tiếp tuyến chung?
Đọc tiếp
Trong hệ trục Oxyz, cho hai mặt cầu (S1)\(\left(x-1\right)^2+\left(y+3\right)^2+\left(z-2\right)^2=49\) và
(S2) \(\left(x-10\right)^2+\left(y-9\right)^2+\left(z-2\right)^2=400\) và mặt phẳng (P) : 4x-3y+mz+22=0 . Có bao nhiêu số
nguyên m để mp (P) cắt hai mặt cầu (S1), (S2) theo giao tuyến là hai đường tròn không có tiếp tuyến chung?
Có một quả bóng hình cầu đặc đường kính 20cm được đặt đứng yên trên mặt phẳng nằm ngang. Người ta lấy một chiếc nón úp vào quả bóng thì thấy đáy nón vừa chạm với mặt phẳng nằm ngang và các đường sinh của mặt nón cũng vừa tiếp xúc với bề mặt của quả bóng. Biết rằng độ rộng của góc ở đỉnh nón là 60^0. Tính thể tích của khối nón giới hạn bởi chiếc nón và mặt phẳng nằm ngang và tính phần không gian bên trong khối nón mà không bị quả bóng chiếm chỗ
Đọc tiếp
Có một quả bóng hình cầu đặc đường kính 20cm được đặt đứng yên trên mặt phẳng nằm ngang. Người ta lấy một chiếc nón úp vào quả bóng thì thấy đáy nón vừa chạm với mặt phẳng nằm ngang và các đường sinh của mặt nón cũng vừa tiếp xúc với bề mặt của quả bóng. Biết rằng độ rộng của góc ở đỉnh nón là \(60^0\). Tính thể tích của khối nón giới hạn bởi chiếc nón và mặt phẳng nằm ngang và tính phần không gian bên trong khối nón mà không bị quả bóng chiếm chỗ
cho tứ diện ABCD với AB=AC=a. BC=b, hai mặt phẳng BCD và ABC cuông góc với nhau và góc BDc bằng 90 độ. xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện ABCD
1>cho S.ABC có tam giác ABC vuông cân tại A, AB=a và SH vuông (ABC) với H là đối xứng của A qua B, SH = 2a .Tính bán kính mặt cầu ngoại tiếp S.ABC và thể tích khối cầu ngoại tiếp đó
Cho 2 mặt phẳng (P) và (Q) vuông góc với nhau, có giao tuyến là \(\Delta\). Trên \(\Delta\) lấy 2 điểm A, B với AB = a. Trong mặt phẳng (P) lấy điểm C, trong (Q) lấy điểm D sao cho AC, BD vuông góc với \(\Delta\). Giả sử AC= BD = AB. Tìm bán kính hình cầu ngoại tiếp tứ diện ABCD
HELP ME!!!!!1 Cho hình chóp S.ABC có đáy là tam giác cân, AB AC a, (SBC) vuông góc với (ABC) và SA SB a. Cmr ∆ SBC vuông. Biết SC x, tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC2 Cho lăng trụ đứng tam giác ABC.A’B’C’ biết AA’ AB a, AC 2a và góc BAC 60⁰. Gọi M A’C ∩ AC’. Tính thể tích tứ diện MBB’C và tính bán kính mặt cầu ngoại tiếp hình lăng trụ.
Đọc tiếp
HELP ME!!!!!
1> Cho hình chóp S.ABC có đáy là tam giác cân, AB = AC = a, (SBC) vuông góc với (ABC) và SA = SB =a. Cmr ∆ SBC vuông. Biết SC= x, tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC
2> Cho lăng trụ đứng tam giác ABC.A’B’C’ biết AA’ = AB = a, AC = 2a và góc BAC = 60⁰. Gọi M = A’C ∩ AC’. Tính thể tích tứ diện MBB’C và tính bán kính mặt cầu ngoại tiếp hình lăng trụ.
cho tứ diện ABCD có AB,BC,CD đôi một vuông góc.Cho AB=\(a\sqrt{2}\),BC=2a.Gọi I là trung điểm của BD. Tính bàn kính mặt cầu tâm I và mặt cầu này tiếp xúc (ACD)
Cho tứ diện ABCD có ABdfrac{asqrt{3}}{2} và các cạnh còn lại đều bằng a . Biết rằng bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng dfrac{asqrt{m}}{n} với m,nin N*; mle15. Tổng Tm+n bằng?A. 15 B. 17 C. 19 D. 21Có gì cho mình xin công thức chung để tính bán kính mặt cầu ngoại tiếp tứ diện luôn ạ, mình cảm ơn nhiều♥
Đọc tiếp
Cho tứ diện ABCD có \(AB=\dfrac{a\sqrt{3}}{2}\) và các cạnh còn lại đều bằng \(a\) . Biết rằng bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng \(\dfrac{a\sqrt{m}}{n}\) với \(m,n\in N\)*; \(m\le15\). Tổng \(T=m+n\) bằng?
A. 15 B. 17 C. 19 D. 21
Có gì cho mình xin công thức chung để tính bán kính mặt cầu ngoại tiếp tứ diện luôn ạ, mình cảm ơn nhiều♥
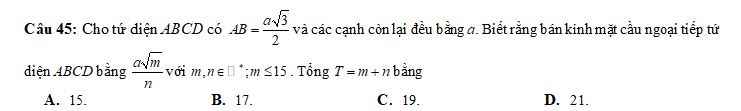
Cho tứ diện đều ABCD cạnh a, đường cao AH, O là trung điểm AH. Bán kính mặt cầu ngoại tiếp tứ giác OBCD là ?










