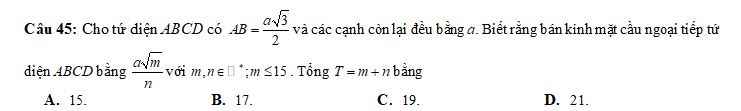Question

Cho 2 mặt phẳng (P) và (Q) vuông góc với nhau, có giao tuyến là \(\Delta\). Trên   \(\Delta\) lấy 2 điểm A, B với AB = a. Trong mặt phẳng (P) lấy điểm C, trong (Q) lấy điểm D sao cho AC, BD vuông góc với  \(\Delta\). Giả sử AC= BD = AB. Tìm bán kính hình cầu ngoại tiếp tứ diện ABCD

 

  

Answer 1

Do \(\left(P\right)\perp\left(Q\right)\) và \(\left(P\right)\cap\left(Q\right)=\Delta\)

và \(DB\perp\left(\Delta\right)\left(DB\in\left(Q\right)\right)\)

Nên \(DB\perp\left(P\right)\Rightarrow DB\perp BC\)

Tương tự ta có :

                \(CA\perp AD\)

Vì \(\widehat{CAD}=\widehat{DBC}=90^0\) nên CD chính là  đường kính hình cầu ngoại tiếp tứ diện ABCD.

Gọi R là bán kính của hinh cầu này thì :

                \(R=\frac{1}{2}CD\)  (1)

Theo định lý Pitagoc trong 2 tam giác vuông CAD, ABD ta có :

        \(CD^2=CA^2+AD^2=CA^2+BA^2+BD^2=3a^2\)

                                         \(\Rightarrow CD=a\sqrt{3}\) (2)

Từ (1) và (2) suy ra \(R=\frac{a\sqrt{3}}{2}\)