Cho tứ diện ABCD có \(AB=\dfrac{a\sqrt{3}}{2}\) và các cạnh còn lại đều bằng \(a\) . Biết rằng bán kính mặt cầu ngoại tiếp tứ diện ABCD bằng \(\dfrac{a\sqrt{m}}{n}\) với \(m,n\in N\)*; \(m\le15\). Tổng \(T=m+n\) bằng?
A. 15 B. 17 C. 19 D. 21
Có gì cho mình xin công thức chung để tính bán kính mặt cầu ngoại tiếp tứ diện luôn ạ, mình cảm ơn nhiều♥
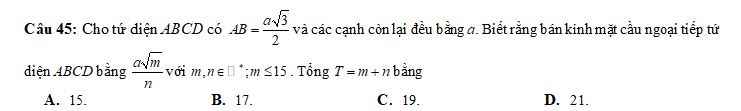
Hóng ké ai đó giải bài nì, ko thì toi xách mông đi hỏi, ngu hình quá :(
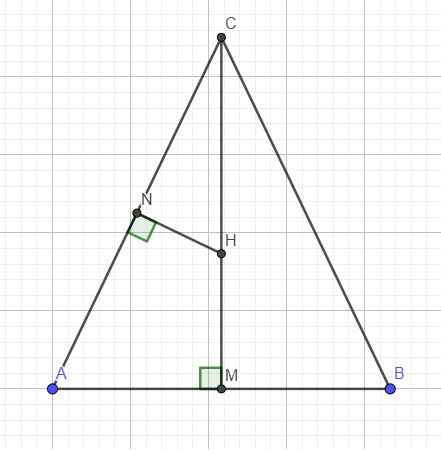
Gọi M là trung điểm AB, do \(DA=DB=DC=a\Rightarrow\) hình chiếu vuông góc H của D lên (ABC) trùng tâm đường tròn ngoại tiếp ABC, hay tâm I của mặt cầu ngoại tiếp tứ diện thuộc đường thẳng DH
Tam giác ABC cân tại C, qua trung điểm N của AC kẻ trung trực cắt CM tại H
\(AM=\dfrac{a\sqrt{3}}{4}\Rightarrow CM=\dfrac{a\sqrt{13}}{4}\) ; \(CH=\dfrac{CN}{cos\widehat{ACM}}=CN.\dfrac{CA}{CM}=\dfrac{2a\sqrt{13}}{13}\)
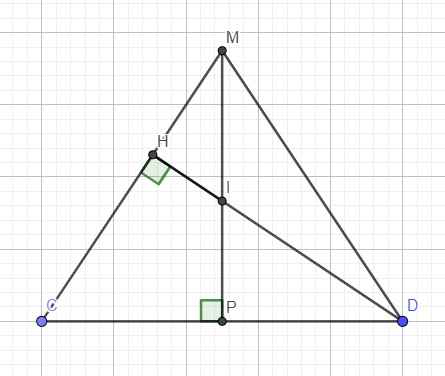
Gọi P là trung điểm CD, do tam giác CDM cân tại M \(\Rightarrow\) CM là trung trực CD
Gọi I là giao điểm PM và DH \(\Rightarrow\) I là tâm mặt cầu ngoại tiếp tứ diện
\(MH=CM-CH=\dfrac{5a\sqrt{13}}{52}\) ; \(MP=\sqrt{MC^2-CP^2}=\dfrac{3a}{4}\)
\(DH=\sqrt{MD^2-MH^2}=\sqrt{MC^2-MH^2}=\dfrac{3a\sqrt{13}}{13}\)
\(IH=MH.tan\widehat{CMP}=MH.\dfrac{CP}{MP}=\dfrac{5a\sqrt{13}}{78}\)
\(R=ID=DH-IH=\dfrac{a\sqrt{13}}{6}\)