§2. Bất phương trình và hệ bất phương trình một ẩn
Các câu hỏi tương tự
Nếu nhân hai vế bất phương trình \(\dfrac{1}{x}\le1\) với \(x\) ta được bất phương trình nào. Bất phương trình nhận được có tương đương với bất phương trình đã cho hay không ? Vì sao ?
Nếu bình phương hai vế (Khử căn thức chứa ẩn) của bất phương trình \(\sqrt{1-x}\le x\) ta nhận được bất phương trình nào ? Bất phương trình nhận được có tương đương bất phương trình đã cho hay không ? Vì sao ?
Cho S là tập hợp tất cả caccs giá trị nguyên của tham ssos m sao cho bất phương trình \(\dfrac{(m+1)x^2+\left(4m+2\right)x+4m+4}{mx^2+2\left(2m+1\right)x+m}\le1\) có tập nghiệm là R . Tính số phần tử của tập hợp S
Bài 1: Tìm m sao cho hệ bất phương trình \(\left\{{}\begin{matrix}x^2-3x-4\le0\\\left(m-1\right)x-2\ge0\end{matrix}\right.\)có nghiệm.
Bài 2: Tìm tất cả giá trị thực của tham số m để hệ bất phương trình \(\left\{{}\begin{matrix}x^2+10x+16\le0\\mx\ge3x+1\end{matrix}\right.\)vô nghiệm.
Viết điều kiện của mỗi bất phương trình đã cho sau đây rồi cho biết các bất phương trình này có tương đương với nhau hay không ?
\(\sqrt{\left(x-1\right)\left(x-2\right)}\ge x\) (1)
\(\sqrt{x-1}.\sqrt{x-2}\ge x\) (2)
Giá trị nhỏ nhất của biểu thức P=4x+16\x^2, x>0 bằng bao nhiêu
Giải bất phương trình dfrac {1} {(x-2)^2} leq dfrac {1} {x-4} Lời giải:Vì mình không giỏi tư duy nên không làm theo cách này, mình tạo bảng xét dấu, nhưng đến đây rồi mình không biết làm sao hết. Nhờ các bạn giúp mình tìm lỗi và giải tiếp. Mình cảm ơn nhiều. Cho mình hỏi là đối với trường hợp dưới mẫu là biểu thức bình phương thì khi tạo bảng xét dấu, biểu thức đó có bỏ bình phương không, hay giữ nguyên và tiếp tục xét.
Đọc tiếp
Giải bất phương trình
\( \dfrac {1} {(x-2)^2} \leq \dfrac {1} {x-4}\)
Lời giải:
Vì mình không giỏi tư duy nên không làm theo cách này, mình tạo bảng xét dấu, nhưng đến đây rồi mình không biết làm sao hết. Nhờ các bạn giúp mình tìm lỗi và giải tiếp. Mình cảm ơn nhiều.

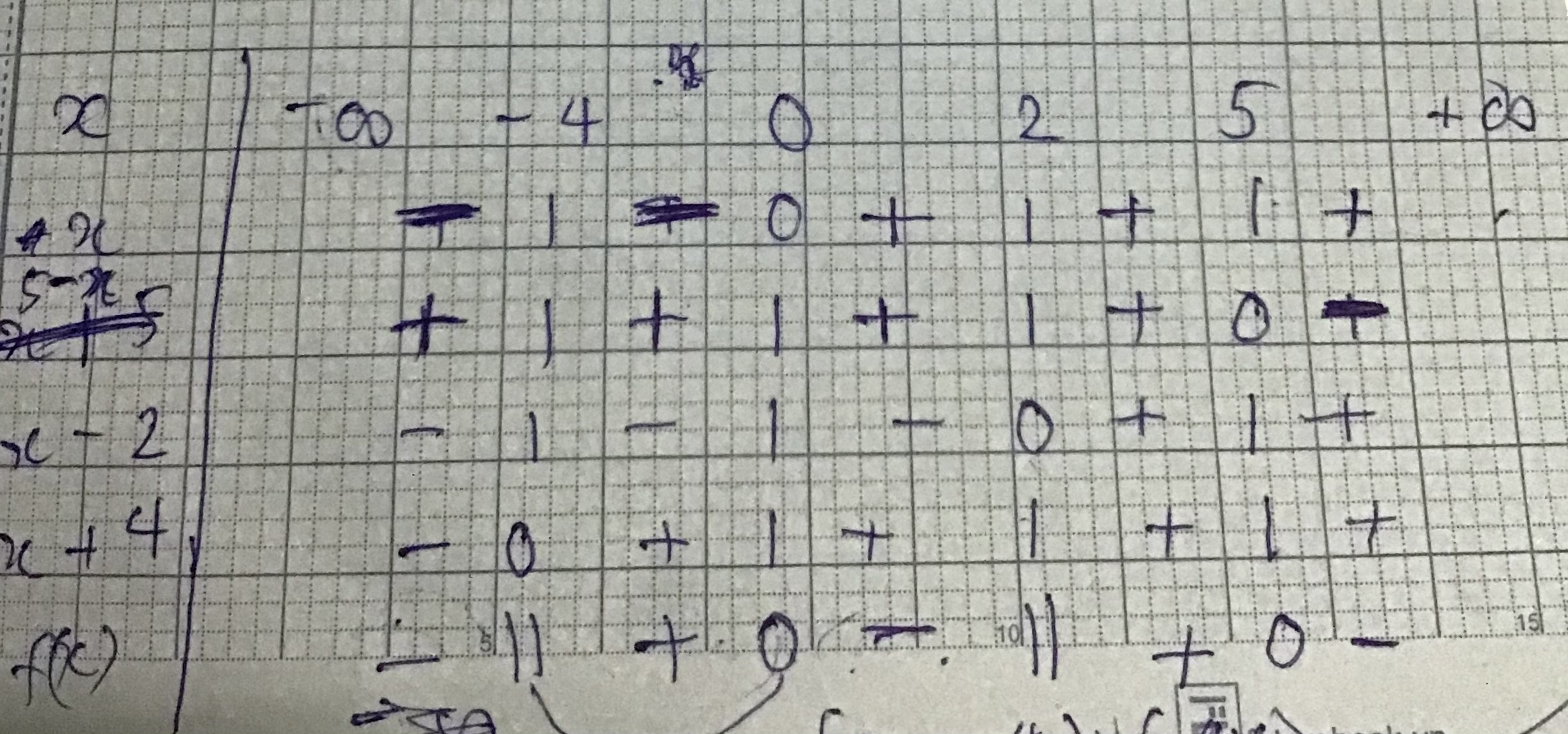

Cho mình hỏi là đối với trường hợp dưới mẫu là biểu thức bình phương thì khi tạo bảng xét dấu, biểu thức đó có bỏ bình phương không, hay giữ nguyên và tiếp tục xét.
Cho Parabol (P) y= x2 +x + 3 và đường thẳng d : y= mx + 2 . Tìm tất cả các giá trị
của tham số m để d cắt P tại 2 điểm phân biệt có hoành độ x 1,x2 , thỏa x12 +x2 2 - 7 ≤ 0
.
f(x)=\(\dfrac{x^2+16}{2x}\)t(x>0) tìm hàm số x đạt giá trị nhỉ nhất thì x nằm trong khoảng bao nhiêu








