Bài 4: Khái niệm hai tam giác đồng dạng
Các câu hỏi tương tự
hình thang ABCD(AB//CD)EG//AB//CD,AE=2/5 ED.
a,Tnhs BG/GC và CG/BC
b.tính EG biết AB=5cm và DC=30cm
Hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC (h.21).
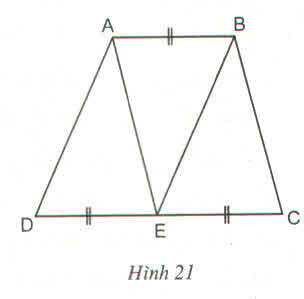
Chứng minh rằng 3 tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)
cho hình thang ABCD có AB=3cm, BC= 10cm, CD=12cm, AD= 5cm, BD= 6cm
C/m ΔABC đồng dạng vs ΔBDC
có vẽ hình
Qua giao điểm O của 2 đường chéo tứ giác ABCD, kẻ 1 đường thẳng tùy ý cắt AB tại M, cắt CD tại N. Đường thẳng qua M song song với CD cắt AC tại E, đường thẳng qua N song song với AB cắt BD tại F. Chứng minh BE//CF
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng là tam giác ABD đồng dạng với tam giác BDC
a) cmr AB song song với CD
b) Tính các độ dài BD, BC biết AB=2cm , AD=3cm , CD=8cm
Giup minh voi

cho tam giác như hình vẽ trên
a, chứng minh:tam giác ABC ~ tam giác MNP.
b, Tam giác ABC ~tam giác MNP theo tỉ số K bằng bao nhiêu ??< kh:~ là đồng dạng >
Cho tam giác ABC có AB=15, AC=8,BC=100.Trên tia AB đặt E sao cho AE=20.Qua E vẽ 1 tia cắt AC tại D sao cho góc AED=góc ACB 1/Cmr tam giác ADE đồng dạng với tam giác ABC
2/ tính các cạnh còn lại của tam giác ADE










