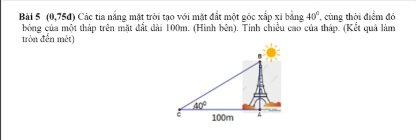
\(\sqrt{x^2-2x+1}=\sqrt{3+2\sqrt{2}}\)
\(\Leftrightarrow\sqrt{\left(x-1\right)^2}=\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(\Leftrightarrow\left|x-1\right|=\sqrt{2}+1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=\sqrt{2}+1\\x-1=-\sqrt{2}-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2+\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Lời giải:
PT $\Leftrightarrow \sqrt{(x-1)^2}=\sqrt{(\sqrt{2}+1)^2}$
$\Leftrightarrow |x-1|=|\sqrt{2}+1|=\sqrt{2}+1$
$\Leftrightarrow x-1=\pm (\sqrt{2}+1)$
$\Leftrightarrow x=2+\sqrt{2}$ hoặc $x=-\sqrt{2}$