Chương I - Căn bậc hai. Căn bậc ba
Các câu hỏi tương tự
1. Tìm tất cả các số tự nhiên \(n\) để phân thức sau tối giản: \(A=\dfrac{2n^2+3n+1}{3n+1}\)
2. Cho các số thực dương x, y, z thỏa mãn \(xy^2z^2+x^2z+y=3z^2\) .Tìm giá trị lớn nhất của biểu thức: \(M=\dfrac{z^4}{1+z^4\left(x^4+y^4\right)}\)
Tìm tất cả các cặp số nguyên dương x,y thỏa mãn \(\left(xy+x+y\right)\left(x^2+y^2+1\right)=30\)
Tìm tất cả số a,b sao cho x=\(\sqrt{3}+1\)là nghiệm của phương trình
Đặt Sn=x1n +x2n+x3n CMR Sn\( \in\)Z
tìm tất cả các cặp số (x,y) thỏa mãn: 5x-2\(\sqrt{x}\left(y+2\right)+y^2+1=0\)
P = \(\frac{\sqrt{x}}{x-1}+\frac{2}{x}-\frac{1}{\sqrt{x}\left(x-1\right)}\)
Tìm tất cả các giá trị dương của x để P nhận giá trị nguyên.
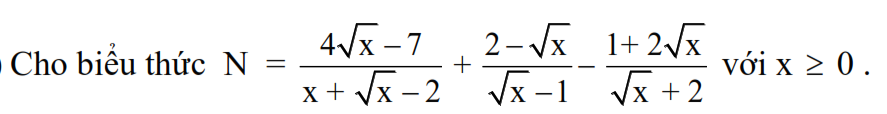
a) Tìm x để N=\(\dfrac{1}{2}\)
b) Tìm x ∈ \(Z\) sao cho N ∈ \(Z\)
c) Tìm GTLN của N
Tìm cặp số nguyên dương x,y thỏa mãn:
\(x\sqrt{2y-1}+y\sqrt{2x-1}=2xy\)
1) Cho a ∈ N thỏa mãn sqrt{a}∈ Q. CM: sqrt{a}∈ N
2) Cho x, y ∈ N thỏa mãn sqrt{x}+sqrt{y} ∈ N
CM: sqrt{x},sqrt{y} ∈ N
3) Tìm x, y nguyên dương thỏa mãn sqrt{x}+sqrt{y}sqrt{x+y}+2
4) Cho n là số nguyên dương thỏa mãn 2+2sqrt{1+12n^2} là số tự nhiên.
CM: 2+2sqrt{1+12n^2}là số chính phương
Đọc tiếp
1) Cho a ∈ N thỏa mãn \(\sqrt{a}\)∈ Q. CM: \(\sqrt{a}\)∈ N
2) Cho x, y ∈ N thỏa mãn \(\sqrt{x}+\sqrt{y}\) ∈ N
CM: \(\sqrt{x},\sqrt{y}\) ∈ N
3) Tìm x, y nguyên dương thỏa mãn \(\sqrt{x}+\sqrt{y}=\sqrt{x+y}+2\)
4) Cho n là số nguyên dương thỏa mãn \(2+2\sqrt{1+12n^2}\) là số tự nhiên.
CM: \(2+2\sqrt{1+12n^2}\)là số chính phương
Cho phương trình \(x^2+x+m-2=0\left(1\right)\). Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm phân biệt x1, x2 thỏa mãn x12-2x1x2-x2=1
Cho biểu thức \(A=\left(\frac{1}{\sqrt{x+2}}+\frac{1}{\sqrt{x}-2}\right).\frac{\sqrt{x}-2}{\sqrt{x}}\)
a,Tìm ĐKXĐ và rút gọn biểu thức A
b,Tìm tất cả các giá trị của x để A>1/2
c,Tìm tất cả các giá trị của x để B=5/2.A là 1 số nguyên












