§1. Hàm số
Các câu hỏi tương tự
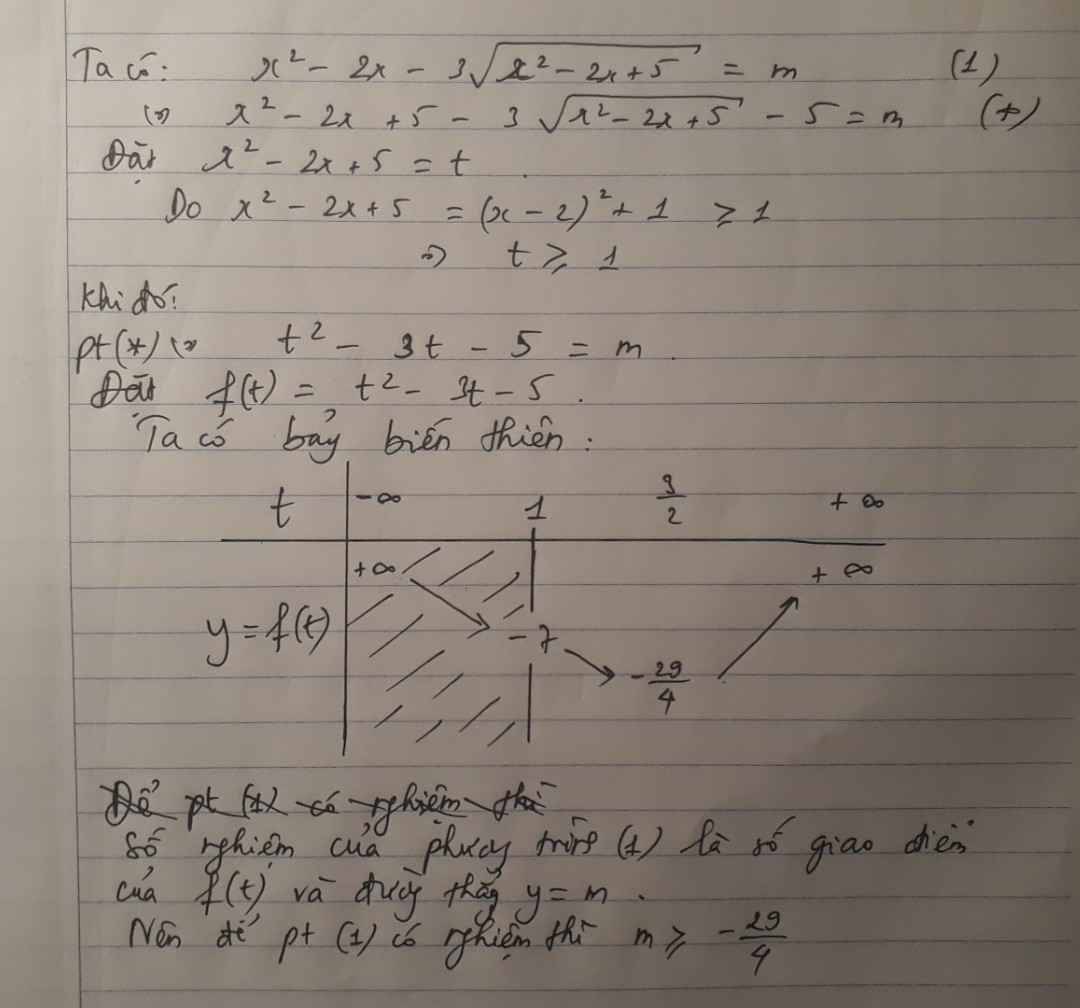
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm :
a) x^2 - 8√x^2+1 +5-m=0
b) x^2 + 2x - 8√x^2+2x+5 +3-m =0
Xem chi tiết
Khảo sát sự biến thiên của hàm số sau:
a;y=f(x)=\(\sqrt{x^2+2x+3}\)
b;y=f(x)=\(\sqrt{x^2-3x+2}\)
c;y=f(x)=\(\sqrt{-5x^2+2x+3}\)
Tìm giá trị nhỏ nhất của m để phương trình \(\sqrt[3]{x^4+2x^2+1}\) - 3\(\sqrt[3]{x^2+1+}+5-m=0\) có nghiệm
xét sự biến thiên của hàm số sau trên tập xác định của nó và lập bảng biến thiên:
a, \(y=-x^2-2x+3\)
b, \(y=\dfrac{x+1}{x-2}\)
- Cho đồ thị hàm số y =|x|- 2 . Tìm toạ độ giao điểm của đồ thị vs trục tung và trục hoành
- vẽ đồ thị hàm số y = -1/2 + | 2x +3|+5/2
Vẽ đồ thị của hàm số y = x ^ 2 - 2x + 2 và nêu các khoảng đồng biến,nghịch biến
x1,hai đường thẳng y(m-1)x + 2 và yx-k song song với nhau khi nào.2, a, Vẽ trên cùng một trục hệ tọa độ Oxy đồ thị các hàm số sau: y-2x+3, yx+2b Tìm tọa độ giao điểm C của hai đồ thị hàm số trênc, Gọi A, B lần lượt là giao điểm của đồ thị 2 hàm số với trục Ox. Tính diện tích tam giác ABC3, Cho đường thẳng y(2-m)x+m+1 (d)Chứng minh rằng với các giá trị m ne2 , các đường thẳng xác định bởi (d) luôn đi qua một điểm cố định? Tìm điểm cố định đó.Giúp mình với.
Đọc tiếp
x1,hai đường thẳng y=(m-1)x + 2 và y=x-k song song với nhau khi nào.
2, a, Vẽ trên cùng một trục hệ tọa độ Oxy đồ thị các hàm số sau: y=-2x+3, y=x+2
b Tìm tọa độ giao điểm C của hai đồ thị hàm số trên
c, Gọi A, B lần lượt là giao điểm của đồ thị 2 hàm số với trục Ox. Tính diện tích tam giác ABC
3, Cho đường thẳng y=(2-m)x+m+1 (d)
Chứng minh rằng với các giá trị m \(\ne\)2 , các đường thẳng xác định bởi (d) luôn đi qua một điểm cố định? Tìm điểm cố định đó.
Giúp mình với.
Cho hàm số: y = x2 + 2x – 3 có đồ thị là parabol (P). Xác định tọa độ đỉnh, trục đối xứng, bề lõm, giao trục Ox , giao trục Oy và vẽ đồ thị (P)
Bài 1:Tìm tập xác định của hàm số sau:
a) yfrac{1-2x}{2x^2-5x+2}
b) yfrac{x}{x-1}+sqrt{2x+4}
c)y frac{sqrt{x-2}}{x^2+2x+1}
d)y frac{3x+1}{x^2-x+1}
e) yfrac{x+3}{2x^2-18}+frac{5}{1+x^2}-2x+1
f) yfrac{x^3-3}{sqrt{x-2}-sqrt{7-3x}}
Bài 2: Tìm m để hàm số yfrac{3x+5}{x^2+3x+m-1}có tập xác định là DR
Đọc tiếp
Bài 1:Tìm tập xác định của hàm số sau:
a) y=\(\frac{1-2x}{2x^2-5x+2}\)
b) y=\(\frac{x}{x-1}+\sqrt{2x+4}\)
c)y= \(\frac{\sqrt{x-2}}{x^2+2x+1}\)
d)y= \(\frac{3x+1}{x^2-x+1}\)
e) y=\(\frac{x+3}{2x^2-18}+\frac{5}{1+x^2}-2x+1\)
f) y=\(\frac{x^3-3}{\sqrt{x-2}-\sqrt{7-3x}}\)
Bài 2: Tìm m để hàm số y=\(\frac{3x+5}{x^2+3x+m-1}\)có tập xác định là D=R