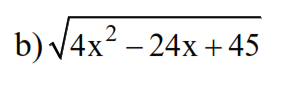`b)sqrt{4x^2-24x+45}`
`=sqrt{(2x)^2-2.2x.6+36+9}`
`=sqrt{(2x-6)^2+9}`
Vì `(2x-6)^2>=0=>(2x-6)^2+9>=9`
`=>sqrt{(2x-6)^2+9}>=sqrt9=3`
Dấu "=" xảy ra khi `2x-6=0<=>2x=6<=>x=3`
Vậy `GTLN{sqrt{4x^2-24x+45}}=3<=>x=3`
\(\sqrt{4x^2-24x+45}=\sqrt{4\left(x-3\right)^2+9}\)
Vì \(4\left(x-3\right)^2\ge0\Rightarrow4\left(x-3\right)^2+9\ge9\)
\(\Rightarrow\sqrt{4x^2-24x+45}\ge\sqrt{9}=3\)
\(ĐTXR\Leftrightarrow x=3\)