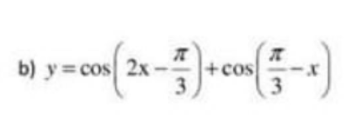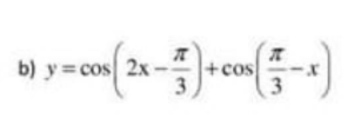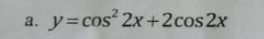Question

tìm gtnn và gtln

Answer 1

Lời giải:
$y=\cos 2x+\cos x-3=2\cos ^2x+\cos x-4$

$=(2\cos ^2x+\cos x-3)-1$

$=(\cos x-1)(2\cos x+3)-1$
Với $x\in [\frac{-\pi}{3}, \frac{\pi}{2}]$ thì:

$\cos x-1\leq 0; 2\cos x+3\geq 0$

$\Rightarrow y\leq 0-1=-1$

Vậy $y_{\max}=-1$

-------------------

$y=2\cos ^2x+\cos x-4$

$\cos x\geq 0$ với mọi $x\in [\frac{-\pi}{3}; \frac{\pi}{2}]$

$\Rightarrow y\geq 2.0+0-4=-4$ 

Vậy $y_{\min}=-4$