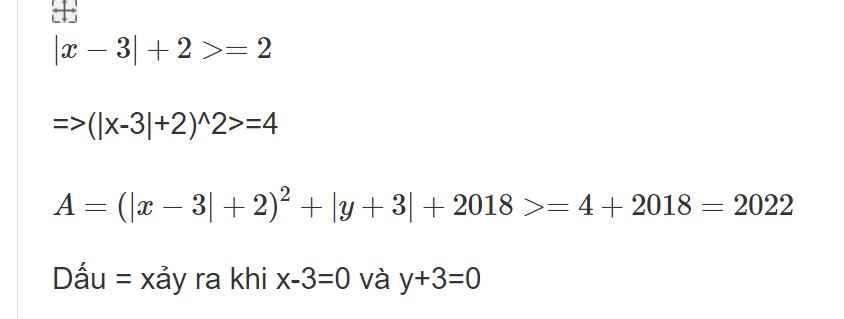Bài 3: Biểu đồ
Các câu hỏi tương tự
Tìm GTNN của biểu thức:
A=\(\left(\left|x-3\right|+2\right)^2+\left|y+3\right|+2018\)
a/Tìm GTNN của biểu thức A=\(\left(2x+\dfrac{1}{3}\right)^4-1\)
b/Tìm GTLN của biểu thức B=\(-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^{2018}+3\)
Tìm x,y:
a/\(x^2+\left(y-\dfrac{1}{10}\right)^4=0\)
b/\(\left(\dfrac{1}{2}x-5\right)^{20}+\left(y^2-\dfrac{1}{4}\right)^{10}\le0\)
1)Tìm x;y;z biết
a) \(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}\) và \(2x+3y-z=50\)
2)Cho \(x\ne0;y\ne0;z\ne0\) và \(x-y-z=0\)
Tính:\(B=\left(1-\dfrac{z}{x}\right).\left(1-\dfrac{x}{y}\right).\left(1+\dfrac{y}{z}\right)\)
Tìm x,y biết:
\(x\left(x-y\right)=\dfrac{3}{10}\)và \(y\left(x-y\right)=-\dfrac{3}{50}\)
So sánh A=\(\left(ax+by\right)^2\)và B=\(\left(a^2+b^2\right)\left(x^2+y^2\right)\) biết rằng a=2,b=-1;x=\(\dfrac{8}{11}\):y=\(-\dfrac{5}{11}\)
Tìm x:
a/\(\left(5x+1\right)^2=\dfrac{36}{49}\)
b/\(\left(x-\dfrac{2}{9}\right)^3=\left(\dfrac{2}{3}\right)^6\)
c/\(\left(8x+1\right)^{2n+1}=5^{2n+1}\left(n\in N\right)\)
Tìm x:
a/\(\left(\dfrac{12}{25}\right)^x\)=\(\left(\dfrac{3}{5}\right)^2-\left(-\dfrac{3}{5}\right)^4\)
b/\(\left(-\dfrac{3}{4}\right)^{3x-1}=\dfrac{256}{81}\)
c/172\(x^2-7^9:98^3=2^{-3}\)
Viết dưới dạng lũy thừa của một số nguyên:
a/\(12^3:\left(3^{-4}.64\right)\)
b/\(\left(\dfrac{3}{7}\right)^5.\left(\dfrac{7}{3}\right)^{-1}.\left(\dfrac{5}{3}\right)^6:\left(\dfrac{343}{625}\right)^{-2}\)
c/\(5^4.125.\left(2,5\right)^{-5}.0,04\)