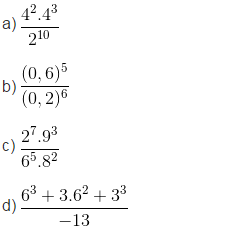a.
\(\frac{4^2\times4^3}{2^{10}}=\frac{4^2\times4^3}{2^{2\times5}}=\frac{4^2\times4^3}{\left(2^2\right)^5}=\frac{4^5}{4^5}=1\)
b.
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\times3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5\times3^5}{\left(0,2\right)^6}=\frac{243}{0,2}=1215\)
c.
\(\frac{2^7\times9^3}{6^5\times8^2}=\frac{2^7\times\left(3^2\right)^3}{\left(2\times3\right)^5\times\left(2^3\right)^2}=\frac{2^7\times3^6}{2^5\times3^5\times2^6}=\frac{3}{2^4}=\frac{3}{16}\)
d.
\(\frac{6^3+3\times6^2+3^3}{-13}=\frac{\left(2\times3\right)^3+3\times\left(3\times2\right)^2+3^3}{-13}=\frac{2^3\times3^3+3\times3^2\times2^2+3^3}{-13}=\frac{8\times3^3+3^3\times4+3^3}{-13}\)\(=\frac{3^3\times\left(8+4+1\right)}{-13}=\frac{27\times13}{-13}=-27\)
a/ \(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^5\right)^2}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)
b/\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,6\right)^5}{\left(0,2\right)^5.\left(0,2\right)}=\left(\frac{0,6}{0,2}\right)^5.\frac{1}{\frac{1}{5}}=3^5.5=243.5=1215\)
c/ \(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3.3^5}{2^7.2^4.3^5}=\frac{3}{16}\)
d/ \(\frac{6^3+3.6^2+3^3}{-13}=\frac{\left(2.3\right)^3+3.\left(2.3\right)^2+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{27.13}{-13}=-27\)