\(I=\int\limits^a_{-a}\frac{3x^2+1}{3^x+1}dx\) (1)
Đặt \(x=-t\Rightarrow dx=-dt\)
\(I=\int\limits^{-a}_a\frac{3^t\left(3t^2+1\right)}{3^t+1}.\left(-dt\right)=\int\limits^a_{-a}\frac{3^x\left(3x^2+1\right)}{3^x+1}dx\) (2)
Cộng (1) với (2):
\(2I=\int\limits^a_{-a}\frac{\left(3x^2+1\right)\left(3^x+1\right)}{3^x+1}dx=\int\limits^a_{-a}\left(3x^2+1\right)dx=\left(x^3+x\right)|^a_{-a}=2a^3+2a\)
\(\Rightarrow I=a^3+a\Rightarrow a^3+a=130\) \(\Rightarrow a=5\)






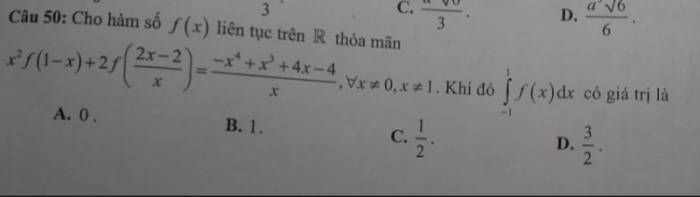 mọi người cho mình hỏi làm sao để xác định được cận của tích phân chạy từ 1 đến 2 ở bài này ?
mọi người cho mình hỏi làm sao để xác định được cận của tích phân chạy từ 1 đến 2 ở bài này ? 






