a) \(f({x_1}) > f({x_2})\)
b) \(f({x_1}) < f({x_2})\)
a) \(f({x_1}) > f({x_2})\)
b) \(f({x_1}) < f({x_2})\)
Xét hàm số \(y = f(x)\) cho bởi bảng sau:
\(x\) | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
\(f(x)\) | 8 | 3 | 0 | -1 | 0 | 3 | 8 |
a) Tìm tập xác định D của hàm số trên.
b) Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với \(x \in D\) và \(y = f(x).\)
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
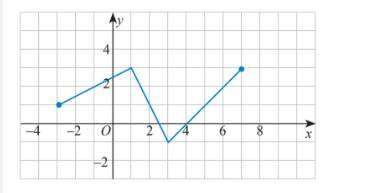
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
Vẽ đồ thị hàm số \(f\left( x \right) = \left| x \right|\) biết rằng hàm số này còn được viết như sau:
\(f(x) = \left\{ \begin{array}{l}x\quad \quad (x \ge 0)\\ - x\quad \;\;(x < 0)\end{array} \right.\)
Vẽ đồ thị hàm số \(f(x) = 3x + 8\).
Tìm tập xác định, tập giá trị và vẽ đồ thị hàm số:
\(f(x) = \left\{ \begin{array}{l} - 1\quad \quad x < 0\\1\;\quad \quad \;{\kern 1pt} x > 0\end{array} \right.\quad \)
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a) \(f(x) = - 5x + 2\)
b) \(f(x) = - {x^2}\)
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt {2x + 7} \)
b) \(f(x) = \frac{{x + 4}}{{{x^2} - 3x + 2}}\)
Tìm tập xác định của các hàm số sau:
a) \(f(x) = \sqrt { - 5x + 3} \)
b) \(f(x) = 2 + \frac{1}{{x + 3}}\)
Số 2 đã trải qua một hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen

Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau:
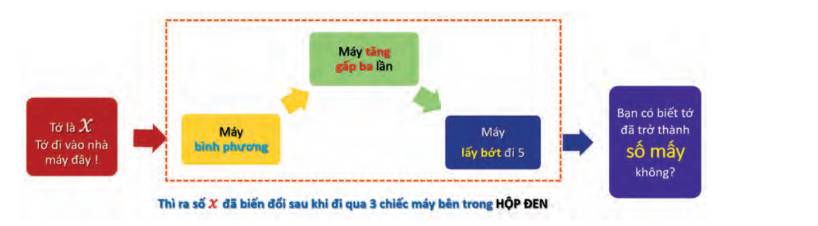
Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết iểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.