Một người nông dân có 15 000 000 đồng để làm một hàng rào hình chữ E dọc theo một con sông bao quanh hai khu đất trồng rau có dạng hai hình chữ nhật bằng nhau (Hình 35). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng/mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng/mét, mặt giáp với bờ sông không phải rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào.
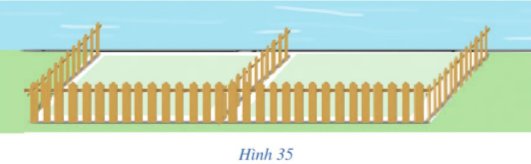
Gọi độ dài của hàng rào song sông với bờ sông là x(m) với x>0
Gọi độ dài của mỗi hàng rào trong ba hàng rào song song nhau là y(m) với y>0
Diện tích đất mà bác nông dân rào được là: \(xy\left( {{m^2}} \right)\)
Tổng chi phí là 15.000.000 đồng nên ta có phương trình:
\(x*60000 + 3y*50000 = 15000000 = > 6x + 15y = 1500\)
Áp dụng bất đẳng thức Cauchy cho hai số dương ta có:
\(6x + 15y \ge 2\sqrt {6x.5y} = > 1500 \ge 2\sqrt {90xy} = > xy \le 6250\)
Vậy diện tích lớn nhất mà bác nông dân có thể tạo rào là 6250\(\left( {{m^2}} \right)\)


