Cho hàm số \(y=f\left(x\right)=\dfrac{1}{4}x^4-x^3+x^2+1\) có đồ thị hàm số hàm số y = f'(x) cho ở Hình 31.
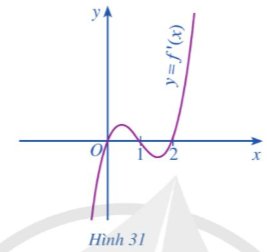
Hàm số y = f(x) đồng biến trên khoảng:
A. (– ∞; 0). B. (0; 1). C. (0; 2). D. (1; 2).
Cho hàm số \(y=f\left(x\right)=\dfrac{1}{4}x^4-x^3+x^2+1\) có đồ thị hàm số hàm số y = f'(x) cho ở Hình 31.

Hàm số y = f(x) đồng biến trên khoảng:
A. (– ∞; 0). B. (0; 1). C. (0; 2). D. (1; 2).
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\dfrac{4x+4}{x^2+2x+1}\) là:
A. 0. B. 1. C. 2. D. 3.
Thảo luận (1)Hướng dẫn giảiTập xác định: \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
Đặt mẫu: \({x^2} + 2x + 1 = 0\) → \(x = - 1\)
Vậy hàm số có TCĐ là \(x = - 1\)
Ta có:
\(\mathop {{\rm{lim}}}\limits_{x \to \pm \infty } \frac{{4x + 4}}{{{x^2} + 2x + 1}} = 0\)
Vậy, hàm số có TCN là: \(y = 0\)
Đáp án C
(Trả lời bởi Nguyễn Quốc Đạt)
Hàm số nào có đồ thị như Hình 32?
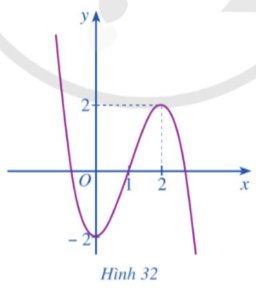
A. y = – x3 + 3x – 2. B. y = – x3 – 2.
C. y = – x3 + 3x2 – 2. D. y = x3 – 3x – 2.
Thảo luận (1)Hướng dẫn giảiXét đồ thị ta thấy hàm số cắt x tại 1 và y tại -2
Thế x=1 vào phương trình
=> Phương trình a có nghiệm x=1 và y=2
=> Chọn A
(Trả lời bởi Nguyễn Quốc Đạt)
Đường cong ở Hình 33 là đồ thị của hàm số nào sau đây?
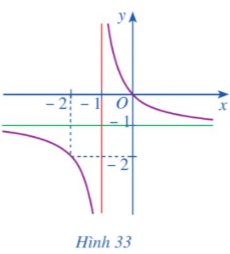
A. \(y=\dfrac{x+1}{x-1}\) B. \(y=\dfrac{-x+1}{x+1}\)
C. \(y=\dfrac{x-1}{x+1}\) D. \(y=\dfrac{-x}{x+1}\)
Thảo luận (1)Hướng dẫn giảiHình 33 có
1 TCĐ \(x = - 1\)
1 TCN \(y = - 1\)
Vậy hàm số cần tìm là: \(y = \frac{{ - x}}{{x + 1}}\)
Đáp án D
(Trả lời bởi Nguyễn Quốc Đạt)
Các đồ thị hàm số ở Hình 34a, Hình 34b đều có đường tiệm cận đứng và đường tiệm cận ngang (hoặc tiệm cận xiên). Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?
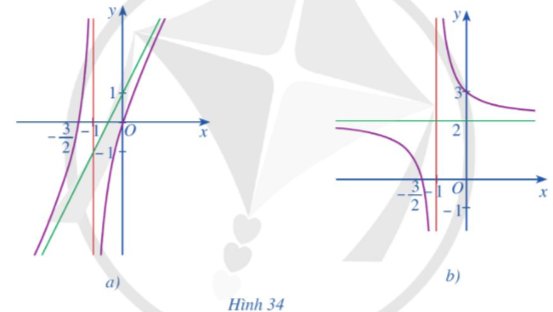
a) \(y=\dfrac{2x+3}{x+1};\) b) \(y=\dfrac{2x-5}{x-1};\) c) \(\dfrac{2x^2+3x}{x+1}.\)
Thảo luận (1)Hướng dẫn giảiXét đồ thị a ta thấy đồ thị đi qua điểm (0;0)
Thay x=0 vào hàm số
=> Thấy C thỏa mãn
=> Chọn C
Xét đồ thị b ta thấy đồ thị đi qua điểm (0;3)Thay x=0 vào hàm số
=> Thấy A thỏa mãn
=> Chọn A
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm các đường tiệm cận ngang và tiệm cận đứng của đồ thị mỗi hàm số sau:
a) \(y=\dfrac{5x+1}{3x-2};\) b) \(y=\dfrac{2x^3-3x}{x^3+1};\) c) \(y=\dfrac{x}{\sqrt{x^2-4}}\).
Thảo luận (1)Hướng dẫn giảiA. \(y = \frac{{5x + 1}}{{3x - 2}}\)
Tập xác định: \(\mathbb{R}\backslash \left\{ {\frac{2}{3}} \right\}\)
Đặt mẫu: \(3x - 2 = 0\) → \(x = \frac{2}{3}\)
Vậy hàm số có TCĐ là: \(x = \frac{2}{3}\)
Ta có:
\(\mathop {{\rm{lim}}}\limits_{x \to \pm \infty } \frac{{5x + 1}}{{3x - 2}} = \frac{5}{3}\)
Vậy, hàm số có TCN là: \(y = \frac{5}{3}\)
B. \(y = \frac{{2{x^3} - 3x}}{{{x^3} + 1}}\)
TXĐ: \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
Đặt mẫu \({x^3} + 1 = 0\) → \(x = - 1\)
Vậy hàm số có TCĐ là: \(x = - 1\)
Ta có:
\(\mathop {{\rm{lim}}}\limits_{x \to \pm \infty } \frac{{2{x^3} - 3x}}{{{x^3} + 1}} = 2\)
Vậy hàm số có TCN là: \(y = 2\)
C. \(y = \frac{x}{{\sqrt {{x^2} - 4} }}\)
TXĐ: \(x \in \left[ { - \infty , - 2} \right] \cup \left[ {2, + \infty } \right]\)
Đặt mẫu \(\sqrt {{x^2} - 4} = 0\) → \(x = - 2;\;x = 2\)
Vậy hàm số có TCĐ là: \(x = - 2;\;x = 2\)
Ta có
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{x}{{\sqrt {{x^2} - 4} }} = 1\)
\(\mathop {{\rm{lim}}}\limits_{x \to - \infty } \frac{x}{{\sqrt {{x^2} - 4} }} = - 1\)
Vậy hàm số có TCN là: \(y = 1;\;y = - 1\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau:
a) \(y=x-3+\dfrac{1}{x^2};\) b) \(y=\dfrac{2x^2-3x+2}{x-1};\) c) \(y=\dfrac{2x^2-x+3}{2x+1}\).
Thảo luận (1)Hướng dẫn giảia) \(y = x - 3 + \frac{1}{{{x^2}}}\)
TCĐ: \({x^2} = 0 \to x = 0\)
Vậy đường tiệm cận đứng của hàm số là \(x = 0\)
TCX:
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{y}{x} = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\left( {x - 3 + \frac{1}{{{x^2}}}} \right)}}{x} = 1\)
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {y - ax} \right) = \mathop {{\rm{lim}}}\limits_{x \to + \infty } x - 3 + \frac{1}{{{x^2}}} - x = - 3\)
Vậy đường tiệm cận xiên của hàm số là \(y = x - 3\)
b) \(y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\)
TCĐ: \(x - 1 = 0 \to x = 1\)
Vậy đường tiệm cận đứng của hàm số là \(x = 1\)
TCX:
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{y}{x} = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\frac{{2{x^2} - 3x + 2}}{{x - 1}}}}{x} = 2\)
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {y - ax} \right) = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{2{x^2} - 3x + 2}}{{x - 1}} - 2x = - 1\)
Vậy đường tiệm cận xiên của hàm số là \(y = 2x - 1\)
c) \(y = \frac{{2{x^2} - x + 3}}{{2x + 1}}\)
TCĐ: \(2x + 1 = 0 \to x = - \frac{1}{2}\)
Vậy đường tiệm cận đứng của hàm số là \(x = - \frac{1}{2}\)
TCX:
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{y}{x} = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\frac{{2{x^2} - x + 3}}{{2x + 1}}}}{x} = 1\)
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {y - ax} \right) = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{2{x^2} - x + 3}}{{2x + 1}} - x = - 1\)
Vậy đường tiệm cận xiên của hàm số là \(y = x - 1\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của mỗi hàm số sau:
a) \(f\left(x\right)=2x^3-6x\) trên đoạn \(\left[-1;3\right]\);
b) \(f\left(x\right)=\dfrac{x^2+3x+6}{x+2}\) trên đoạn \(\left[1;5\right]\);
c) \(f\left(x\right)=\dfrac{\ln\left(x+1\right)}{x+1}\) trên đoạn \(\left[0;3\right];\)
d) \(f\left(x\right)=2\sin3x+7x+1\) trên đoạn \(\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\).
Thảo luận (1)Hướng dẫn giảia) \(f\left( x \right) = 2{x^3} - 6x\) trên đoạn \(\left[ { - 1;3} \right]\)
Tìm điểm cực trị: \(f'\left( x \right) = 0 \to 6{x^2} - 6 = 0 \to x = - 1, x = 1\)
So sánh giá trị hàm số tại các điểm cực trị và hai đầu mút của đoạn:
\(f\left( { - 1} \right) = 2{( - 1)^3} - 6\left( { - 1} \right) = - 2 + 6 = 4\)
\(f\left( 1 \right) = 2{(1)^3} - 6\left( 1 \right) = 2 - 6 = - 4\)
\(f\left( 3 \right) = 2{(3)^3} - 6\left( 3 \right) = 54 - 18 = 36\)
Vậy GTNN của hàm số trên đoạn \(\left[ { - 1;3} \right]\) là \( - 4\) (tại \(x = 1\)), và GTLN là 36 (tại \(x = 3\))
b) \(f\left( x \right) = \frac{{{x^2} + 3x + 6}}{{x + 2}}\) trên đoạn \(\left[ {1;5} \right]\)
\(f'(x) = \frac{{{x^2} + 4x}}{{{{(x + 2)}^2}}} = 0 \Leftrightarrow x = 0\). Khi đó trên đoạn [1;5] không tồn tại x để f’(x) = 0.
So sánh giá trị hàm số tại hai đầu mút của đoạn:
\(f\left( 1 \right) = \frac{{{1^2} + 3.1 + 6}}{{1 + 2}} = \frac{{10}}{3};f\left( 5 \right) = \frac{{{5^2} + 3.5 + 6}}{{5 + 2}} = \frac{{46}}{7}\)
Vậy GTNN của hàm số trên đoạn \(\left[ {1;5} \right]\) là \(\frac{{10}}{3}\) (tại \(x = 1\)), và GTLN là \(\frac{{46}}{7}\) (tại \(x = 5\))
c) \(f\left( x \right) = \frac{{In\left( {x + 1} \right)}}{{x + 1}}\) trên đoạn \(\left[ {0;3} \right]\)
So sánh giá trị hàm số:
\(f\left( 0 \right) = \frac{{\ln \left( {0 + 1} \right)}}{{0 + 1}} = 0; f(e - 1) = \frac{1}{{e + 1}}; f\left( 3 \right) = \frac{{\ln \left( {3 + 1} \right)}}{{3 + 1}} = \frac{{\ln \left( 2 \right)}}{2}\)
Vậy GTNN của hàm số trên đoạn \(\left[ {0;3} \right]\) là 0 (tại \(x = 0\)), và GTLN là \(\frac{{\ln \left( 2 \right)}}{2}\) (tại \(x = 3\))
d) \(f\left( x \right) = 2sin3x + 7x + 1\) trên đoạn \(\left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]\)
\(f'(x) = 6\cos 3x + 7\). Khi đó trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) ta có f’(x) > 0, hàm số đồng biến
So sánh giá trị hàm số tại hai đầu mút của đoạn:
\(f\left( { - \frac{\pi }{2}} \right) = 2\sin \left( {3\left( { - \frac{\pi }{2}} \right)} \right) + 7\left( { - \frac{\pi }{2}} \right) + 1 = 3 - \frac{{7\pi }}{2}\)
\(f\left( {\frac{\pi }{2}} \right) = 2\sin \left( {3\left( {\frac{\pi }{2}} \right)} \right) + 7\left( {\frac{\pi }{2}} \right) + 1 = - 1 + \frac{{7\pi }}{2}\)
Vậy GTNN của hàm số trên đoạn \(\left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]\) là \(3 - \frac{{7\pi }}{2}\) (tại \(x = \frac{{ - \pi }}{2}\)), và GTLN là \( - 1 + \frac{{7\pi }}{2}\) (tại \(x = \frac{\pi }{2}\))
(Trả lời bởi Nguyễn Quốc Đạt)
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) \(y=x^3-3x^2+2;\) b) \(y=-x^3+3x^2-6x;\)
c) \(y=\dfrac{3x-2}{x-2};\) d) \(y=\dfrac{x}{2x+3};\)
e) \(y=\dfrac{x^2+2x+4}{x};\) g) \(y=\dfrac{x^2+4x+3}{x+2}\).
Thảo luận (1)Hướng dẫn giải\(a,\;y = {x^3} - 3{x^2} + 2\)
TXD : R
\(y' = 3{x^2} - 6x\)
Cho y= 0 => \(\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
Bảng biến thiên:
Đồ thị hàm số:
Hàm số đồng biến trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\)
Hàm số nghịch biến trong khoảng (0;2)
\(\;b,\;y = - {x^3} + 3{x^2} - 6x\)
TXD: R
\(y' = \; - 3{x^2} + 6x - 6\)
Bảng biến thiên:
Đồ thị hàm số
Hàm số nghịch biến trên R
\(c,y = \frac{{3x - 2}}{{x - 2}}\)
TXD: R/2
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{3x - 2}}{{x - 2}} = 3 = > TCN\;y = 3\)
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{3x - 2}}{{x - 2}} = - \infty \)
Bảng biến thiên:
Đồ thị hàm số:
Hàm số nghịch biến trên khoảng R
\(d,y = \frac{x}{{2x + 3}}\)
TXD: R \ {\( - \frac{3}{2}\)}
TCN \(y = \frac{1}{2}\)
TCD \(x = - \frac{3}{2}\)
Bảng biến thiên
Đồ thị hàm số:
\(e,y = \frac{{{x^2} + 2x + 4}}{x}\)
\(TXD:\mathbb{R}\backslash \{ 0\} \)
TCD: x = 0.
Không có tiệm cận ngang.
Có thể viết hàm số đã cho dưới dạng: \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 + \frac{4}{x}\), suy ra:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{x} = 0.\\\mathop {\lim }\limits_{x \to - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{4}{x} = 0.\end{array}\)
Do đó, đồ thị hàm số có \(y = x + 2\) là tiệm cận xiên.
\(y' = \frac{{\left( {2x + 2} \right)x - \left( {{x^2} + 2x + 4} \right)}}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}}\).
Cho y’=0 => x=\( \pm 2\).
Bảng biến thiên:
Đồ thị hàm số:
g, \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\)
TXD: \(\mathbb{R}\backslash \{ - 2\} \). \[\]
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \). Đồ thị àm số không có tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to - {2^ + }} y = - \infty ,\mathop {\lim }\limits_{x \to - {2^ - }} y = + \infty \). Đồ thị hàm số có \(x = - 2\) là tiệm cận đứng.
Có thể viết hàm số đã cho dưới dạng: \(y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 - \frac{1}{{x + 2}}\), suy ra:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 1}}{{x + 2}} = 0.\\\mathop {\lim }\limits_{x \to - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1}}{{x + 2}} = 0.\end{array}\)
Do đó, đồ thị hàm số có \(y = x + 2\) là tiệm cận xiên.
Bảng biến thiên:
Đồ thị hàm số:
(Trả lời bởi Nguyễn Quốc Đạt)
Một trang sách có dạng hình chữ nhật với diện tích là 384 cm2. Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?
Thảo luận (1)Hướng dẫn giảiGiả sử chiều dài của trang sách là x và chiều rộng là y. Theo đề bài, diện tích của trang sách là:
$xy~=~384~cm{}^\text{2}$
Khi để lề trên và lề dưới đều là 3 cm, lề trái và lề phải đều là 2 cm thì diện tích phần in chữ sẽ là:
\(\left( {x - 2.3} \right)\left( {y - 2.2} \right)\; = \;\left( {x - 6} \right)\left( {y - 4} \right)\)
Ta có: \(x = \frac{{384}}{y}\) (1)
Thay x vào phương trình \(\left( {x - 6} \right)\left( {y - 4} \right)\) ta thu được \(\left( {x - 6} \right)\left( {\frac{{384}}{x} - 4} \right)\)
\(f\left( x \right) = \;\left( {x - 6} \right)\left( {\frac{{384}}{x} - 4} \right)\)
$\to f\left( x \right)=-4+\left( \frac{2304}{{{x}^{2}}} \right)$
$f\left( x \right)=0\to -4+\left( \frac{2304}{{{x}^{2}}} \right)=0\to x=24$
Thế vào (1): \(x = 24 \to y = 16\)
Vậy kích thước của trang sách có chiều dài 24 cm, chiều rộng 16 cm thì phần in chữ trên trang sách có diện tích lớn nhất
(Trả lời bởi Nguyễn Quốc Đạt)