Question

mọi người giúp mình giải nghiệm nguyên của phương trình này với ạ :/
x³ - 6xy + y³ = 8

 

Answer 1

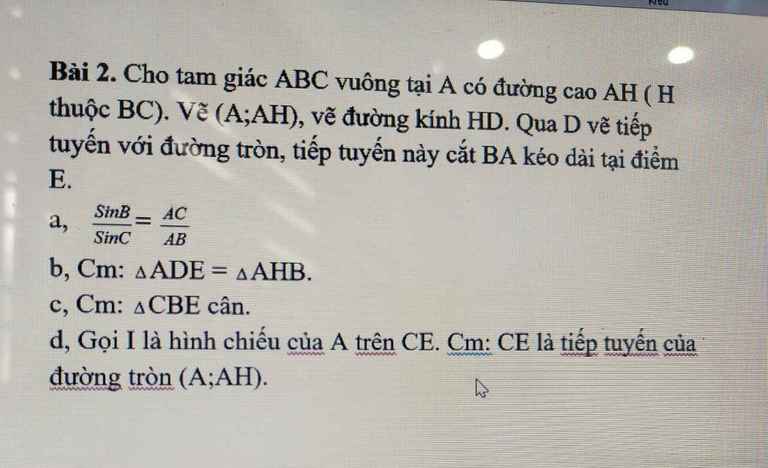
x³ - 6xy + y³ = 8

<=> (x + y)³ - 3xy(x + y) - 6xy + 8 = 16

<=> (x + y + 2)(x² + y² - xy - 2x - 2y + 4) = 16

<=> \(\left(x+y+2\right)\left[\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\right]=16\)

Nhận thấy \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\ge0\)

=> x + y + 2 > 0

Khi đó 16 = 1.16 = 2.8 = 4.4

Lập bảng 

x + y + 2	1	16	4	2	8
\(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\)	16	1	4	8	2
x
y	|

 Đến đó bạn thế x qua y rồi làm tiếp nha