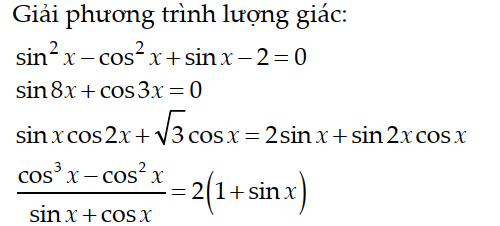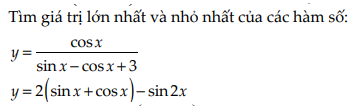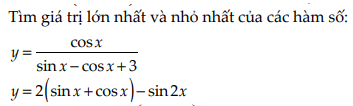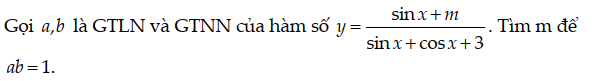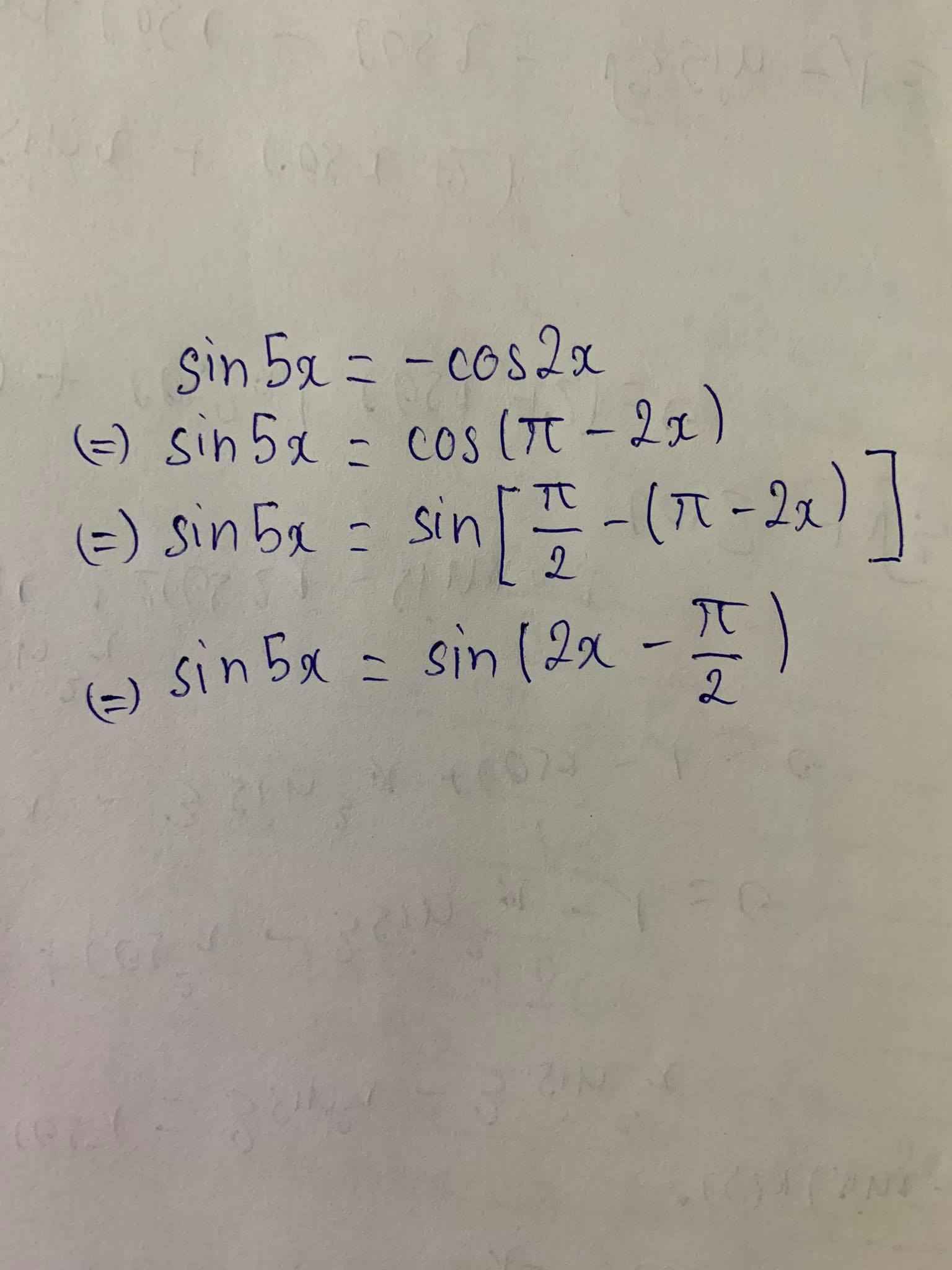1/
PT $\Leftrightarrow \sin ^2x-(1-\sin ^2x)+\sin x-2=0$
$\Leftrightarrow 2\sin ^2x+\sin x-3=0$
$\Leftrightarrow (\sin x-1)(2\sin x+3)=0$
$\Leftrightarrow \sin x=1$ (chọn) hoặc $\sin x=-\frac{3}{2}< -1$ (loại)
Vậy $\sin x=1$
$\Leftrightarrow x=\frac{\pi}{2}+2k\pi$ với $k$ nguyên.
4/
ĐKXĐ: $\tan x\neq -1$
PT $\Rightarrow \cos ^2x(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin ^2x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (1-\sin x)(1+\sin x)(\cos x-1)=2(\sin x+1)(\sin x+\cos x)$
$\Leftrightarrow (\sin x+1)[(1-\sin x)(\cos x-1)-2(\sin x+\cos x)]=0$
$\Leftrightarrow (\sin x+1)(-1-\sin x\cos x-\sin x-\cos x)=0$
$\Leftrightarrow (\sin x+1)^2(\cos x+1)=0$
Nếu $\sin x=-1\Rightarrow x=\frac{-\pi}{2}+2k\pi$ với $k$ nguyên (tm)
Nếu $\cos x=-1\Rightarrow x=\pi +2k\pi$ với $k$ nguyên.
2/
$\sin 8x+\cos 3x=0$
$\Leftrightarrow \sin 8x=-\cos 3x=\cos (\pi -3x)=\sin [\frac{\pi}{2}-(\pi -3x)]=\sin (3x-\frac{\pi}{2})$
\(\Rightarrow \left[\begin{matrix} 8x=3x-\frac{\pi}{2}+2k\pi\\ 8x=\pi -(3x-\frac{\pi}{2})+2k\pi\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{1}{5}(\frac{-\pi}{2}+2k\pi)\\ x=\frac{1}{11}(\frac{3}{2}\pi +2k\pi)\end{matrix}\right.\) với $k$ nguyên.
3/
PT $\Leftrightarrow \sin x(2\cos ^2x-1)+\sqrt{3}\cos x=2\sin x+2\sin x\cos ^2x$
$\Leftrightarrow \sqrt{3}\cos x=3\sin x$
$\Leftrightarrow \cos x-\sqrt{3}\sin x=0$
$\Leftrightarrow \frac{1}{2}\cos x-\frac{\sqrt{3}}{2}\sin x=0$
$\Leftrightarrow \sin \frac{\pi}{6}\cos x-\cos \frac{\pi}{6}\sin x=0$
$\Leftrightarrow \sin (\frac{\pi}{6}-x)=0$
$\Leftrightarrow \frac{\pi}{6}-x=k\pi$ với $k$ nguyên
$\Leftrightarrow x=\pi (\frac{1}{6}-k)$ với $k$ nguyên bất kỳ.
sinx.cos2x + \(\sqrt{3}\)cosx = 2sinx + sin2x.cosx
⇔ sin2x.cosx - sinx.cos2x - \(\sqrt{3}\)cosx + 2sinx = 0
⇔ sinx - \(\sqrt{3}\)cosx + 2sinx = 0
⇔ 3sinx - \(\sqrt{3}\)cosx = 0
⇔ tanx = \(\dfrac{\sqrt{3}}{3}\)
⇔ x = \(\dfrac{\pi}{6}+k.\pi\)