Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Các câu hỏi tương tự
1,y=3x-1/x-3 trên[0;2]
2,căn (100-x2) trên[-6;8]
3,căn(2+x)+căn(4-x)
4,2sin2x-cosx+1
5,sin3 x+cos3 x
6,y=2sinx-1/sinx+2
7,1/cos2 x+cosx+1
tìm max, min a) ydfrac{sqrt{x-1}}{x} trên [1;5]b) ydfrac{x+3}{sqrt{x^2+1}} trên [1;3]c) ysin^2x-cos x+1d) ysin^3x-3sin^2x+2 a0
Đọc tiếp
tìm max, min
a) y=\(\dfrac{\sqrt{x-1}}{x}\) trên \([1;5]\)
b) y=\(\dfrac{x+3}{\sqrt{x^2+1}}\) trên \([1;3]\)
c) y=\(\sin^2x-\cos x+1\)
d) y=\(\sin^3x-3\sin^2x+2\)
a0
Tìm Max, Min của hàm số:1) ydfrac{x+1+sqrt{x-1}}{x+1+2sqrt{x-1}}2) ysin^{2016}x+cos^{2016}x 3) y2cos x-dfrac{4}{3}cos^3x trên left[0;dfrac{pi}{2}right]4) ysin2x-sqrt{2}x+1,xinleft[0;dfrac{pi}{2}right]5) ydfrac{4-cos^2x}{sqrt{sin^4x+1}},xinleft[-dfrac{pi}{3};dfrac{pi}{3}right]
Đọc tiếp
Tìm Max, Min của hàm số:
1) \(y=\dfrac{x+1+\sqrt{x-1}}{x+1+2\sqrt{x-1}}\)
2) \(y=\sin^{2016}x+\cos^{2016}x\)
3) \(y=2\cos x-\dfrac{4}{3}\cos^3x\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
4) \(y=\sin2x-\sqrt{2}x+1,x\in\left[0;\dfrac{\pi}{2}\right]\)
5) \(y=\dfrac{4-cos^2x}{\sqrt{sin^4x+1}},x\in\left[-\dfrac{\pi}{3};\dfrac{\pi}{3}\right]\)
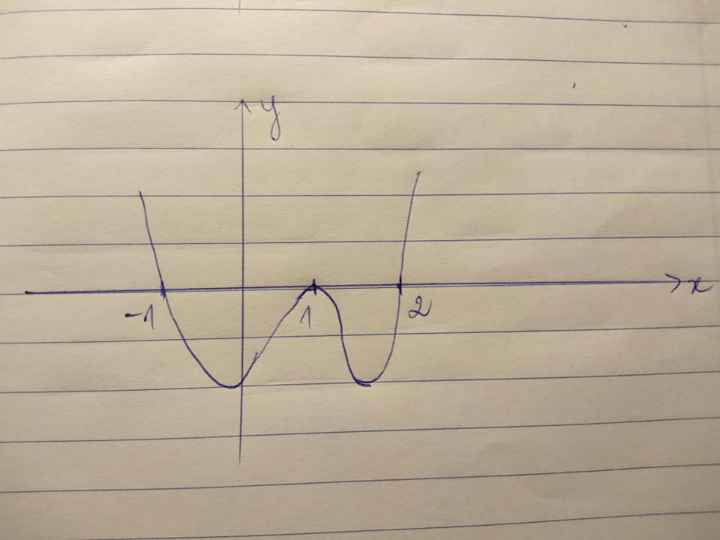
Cho hàm số y=f(x) liên tục trên R có đồ thị y=f '(x) như hình vẽ:
a)Tìm min, max của hàm số g(x)=f(\(\sqrt{8-x^2-2x}-1\))
b)Xác định khoảng đb, nb, cực đại, cực tiểu của g(x)=f(x2+x)
1. Tìm max:y= sinx - \(\sqrt{3}\)cosx
2. Tìm max y= cos2x+3sin2x+2sinx
3. Cho 2 số thực x,y thỏa mãn (x-y+1)2+5(x-y+1)+(x-1)2+6. Đặt P= 3y-3x-(x-1)2. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất. Tính M+m.
Cho a;b;c>=0 thỏa mãn : \(3\left(a^2+b^2+c^2\right)+ab+bc+ac=12\)
Tìm min max của \(P=\dfrac{a^2+b^2+c^2}{a+b+c}+ab+bc+ac\)
1. cho x,y\(\ge\)0 và x2 + y2 + xy = 3 .tìm min, max của T = x3 + y3 - x2 - y2
2. tìm min, max của y = sinpx\(\times\)cosqx, x \(\in\) (0;\(\dfrac{\pi}{2}\) ) ; p,q \(\in\) N*
1) Hàm số y=x√3–2sinx đạt GTNN trên [0;2π] tại x bằng
2)Tìm GTLN của hs
y=(x-6).\(\sqrt{x^2+3}\)trên đoạn [1;2]
3)Hàm số y=x3–2mx2–m+2 đạt MAX là 6 trên đoạn [1;3]
tìm max,min bằng cách đặt ẩn phụ:
a)y=\(\dfrac{1}{cos^4x}+\dfrac{2}{1-cos^4x}\)
b)y=\(\dfrac{sinx+1}{Sin^2x+sinx+1}\)
c)y=\(cos^2x+\dfrac{1}{cos^2x}+cosx+\dfrac{1}{cosx}+1\)










