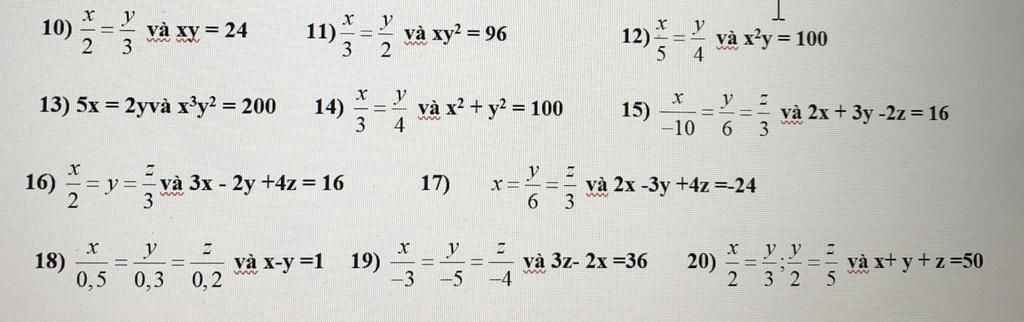14) \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}\)
Theo tính chất của DTSBN, ta được :
\(\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=4.3^2=36\\y^2=4.4^2=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)
Vì x,y cùng dấu nên cặp số (x ; y) = (6 ; 8) ; (-6 ; - 8)
12, Ta có : \(\dfrac{x}{5}=\dfrac{y}{4}\)
\(\Rightarrow y=\dfrac{4}{5}x\)
- Thay y vào biểu thức trên ta được ; \(\dfrac{4}{5}x^3=100\)
\(\Rightarrow x=5\)
\(\Rightarrow y=4\)
Vậy...
14, Ta có : \(\dfrac{x}{3}=\dfrac{y}{4}\)
\(\Rightarrow\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{25}=4\) ( Tính chất dãy tỉ số bằng nhau )
\(\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)
Vậy ...
16) Ta có: \(\dfrac{x}{2}=y=\dfrac{z}{3}\)
\(\Leftrightarrow\dfrac{x}{2}=\dfrac{y}{1}=\dfrac{z}{3}\)
\(\Leftrightarrow\dfrac{3x}{6}=\dfrac{2y}{2}=\dfrac{4z}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{6}=\dfrac{2y}{2}=\dfrac{4z}{12}=\dfrac{3x-2y+4z}{6-2+12}=\dfrac{16}{16}=1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=1\\y=1\\\dfrac{z}{3}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\\z=3\end{matrix}\right.\)
13) Ta có: 5x=2y
nên \(\dfrac{x}{2}=\dfrac{y}{5}\)
Đặt \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k\\y=5k\end{matrix}\right.\)
Ta có: \(x^3y^2=200\)
\(\Leftrightarrow\left(2k\right)^3\cdot\left(5k\right)^2=200\)
\(\Leftrightarrow8k^3\cdot25k^2=200\)
\(\Leftrightarrow k^5=1\)
hay k=1
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k=2\cdot1=2\\y=5k=5\cdot1=5\end{matrix}\right.\)