Bài 4: Khái niệm hai tam giác đồng dạng
Các câu hỏi tương tự
Hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC (h.21).
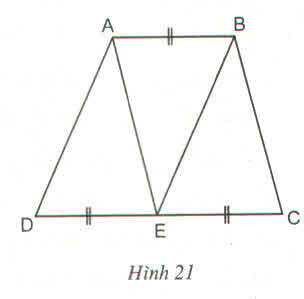
Chứng minh rằng 3 tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)
Hình thang ABCD(AB//CD) có CD=2AB. Gọi E là trung điểm của CD. Chứng minh rằng ba tam giác ADE, ABE, BEC đồng dạng với nhau
Cho hình thang ABCD có AB = AD = 1/2 CD. Gọi M là trung điểm của CD. Gọi H là gia điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh DB vuông góc BC
c) CM: tam giác ADH đồng dạng với tamn giác CDB
d) Biết AB=2,5cm;BD=4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD
giúp mk vs
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ
cho tam giác ABC nhọn, AB<AC .Trên cạnh AB lấy điểm D(D khác A và B),trên cạnh AC lấy điểm E sao cho góc ADE = ACB
a) CM : tam giác ADE đồng dạng tam giác ACB
b)Gọi i là giao điểm của BC và DE. CM: IB.IC=ID.IE
c)Lấy M là trung điểm BC . CM \(\dfrac{AD.AB}{AE.AM}\) =2
Cho tam giác ABC cân tại A. Gọi M là trung điểm của cạnh đáy BC, N là hình chiếu vuông góc của M trên cạnh AC và O là trung điểm của MN.
Chứng minh rằng:
1/ Tam giác AMC đồng dạng với tam giác MNC;
2/ AM.NC=OM.BC
3/AO vuông góc với BN
cho tam giác ABC nhọn. Trên tia đối của tia BA lấy điểm D sao cho 2BD=BA. Trên tia đối của tia CA lấy điểm E sao cho 2CE=CA. Chứng minh tam giác ABC đồng dạng với tam giác ADE
cho hình thang abcd (ab//cd) có m là giao điểm của ad và c, n là giao điểm của hai đường chéo .Gọi i và k theo thứ tự là giao điểm cua mn vói ab và cd.Chứng minh rằng :
a)ai/dk=ib/kc,ai/kc=ib/dk
b)i là trung điểm của ab,k là trung điểm của cd
cho tam nhọn abc (ab nhỏ hơn ac) các đương cao ad be cf cắt nhau tại h
1.chứng minh tam giác eab đồng dạng với tam giác afc và ae.ac=af.ab
2.gọi I là trung điểm của canh BC .Đường thẳng đi qua I và vuông góc với IH cắt AC ,AH,AB lần luotj tại M,K,N
A.chứng minh AM.BI-BH.AK
B.chứng minh rằng NK/EI=MN/BC










