Question

hellp meeeeeeeeeeeeeeeee

Answer 1

Câu 1:

`a,`

Thay `x=1` vào đa thức `A(x)`

\(3\cdot1^2+3\cdot1-6\)

`= 3+3-6`

`= 6-6=0`

Vậy, `x=1` là nghiệm của đa thức `A(x)`.

`b,`

`A(x)+B(x)=`\((3x^2+3x-6)+(x^2-2x+5)\)

`= 3x^2+3x-6+x^2-2x+5`

`= (3x^2+x^2)+(3x-2x)+(-6+5)`

`= 4x^2+x-1`

Answer 2

Bạn tách bài ra hỏi dkhong ạ ;-;?

Answer 3

6:

a: Xet ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

b: AD=ED
ED<DC
=>AD<DC

Answer 4

Câu `2:`

Ta có: \(AB=10 cm, BC = 8cm, AC = 6cm\)

`-> ` `\text {AB > BC > AC (10 > 8 > 6)}`

`@` Theo định lý quan hệ giữa góc và cạnh đối diện

`->`\(\widehat {C}>\widehat {A}>\widehat {B}.\)

Answer 5

Câu `3:`

Ta có: `x/3=y/9 -> (2x)/6=y/9`

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

`(2x)/6=y/9=(2x-y)/(6-9)=-2/-3`

`-> x/3=y/9=2/3`

`-> x=3*2/3=2, y=9*2/3=6`

Answer 6

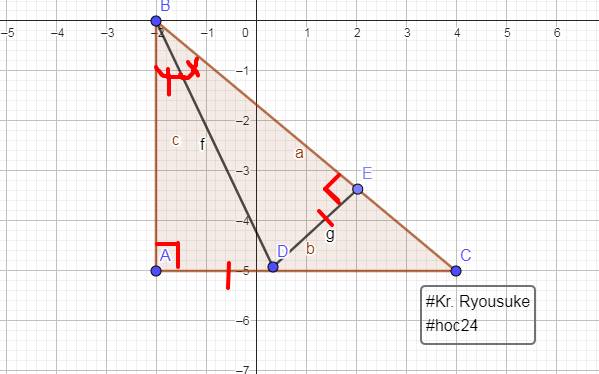
Câu `5:`

`a,`

Xét `2 \Delta` vuông `ABD` và `EBD`:

`\text {BD chung}`

$\widehat {ABD} = \widehat {EBD} (\text {tia phân giác} \widehat {ABE})$

`=> \Delta ABD = \Delta EBD (ch-gn)`

`b,`

Vì `\Delta ABD = \Delta EBD (a)`

`-> \text {AD = DE (2 cạnh tương ứng)}` `(1)`

Xét `\Delta EDC`:

$\widehat {DEC} = 90^0$

`@` Theo định lý quan hệ giữa góc và cạnh đối diện

`-> \text {DC là cạnh lớn nhất}`

`-> \text {DC > DE}` `(2)`

Từ `(1)` và `(2)`

`-> \text { DC > DA (đpcm).}`