f) \(\frac{2.6^9-2^5.18^4}{2^6.6^8}=\frac{2.\left(2.3\right)^9-2^5.\left(3^2.2\right)^4}{2^6.\left(2.3\right)^8}=\frac{2.2^9.3^9-2^5.3^8.2^4}{2^6.2^8.3^8}=\frac{2^{10}.3^9-2^9.3^8}{2^{14}.3^8}=\frac{2^9.3^8\left(2.3-1\right)}{2^{14}.3^8}\)
\(=\frac{5}{2^5}=\frac{5}{32}\)
h) \(\frac{4^6.9^5+6^9.120}{8^4.3^{12}-6^{11}}=\frac{\left(2^2\right)^6.\left(3^2\right)^5+\left(2.3\right)^9.2^3.3.5}{\left(2^3\right)^4.3^{12}-\left(2.3\right)^{11}}=\frac{2^{12}.3^{10}+2^9.3^9.2^3.3.5}{2^{12}.3^{12}-2^{11}.3^{11}}=\frac{2^{12}.3^{10}+2^{12}.3^{10}.5}{2^{11}.3^{11}\left(2.3-1\right)}\)
\(=\frac{2^{12}.3^{10}\left(1+5\right)}{2^{11}.3^{11}.5}=\frac{2.6}{3.5}=\frac{12}{15}=\frac{4}{5}\)






 giúp mình với ạ câu nào cũng được ạ
giúp mình với ạ câu nào cũng được ạ






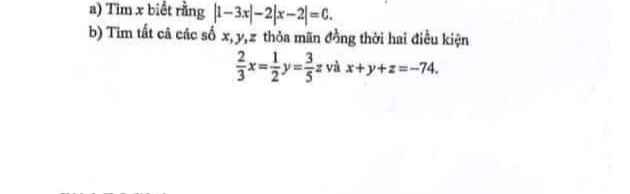

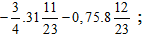 giúp mình với ạ
giúp mình với ạ
