a/ \(\left(\frac{2}{5}+\frac{2}{7}-\frac{2}{11}\right):\left(\frac{3}{7}-\frac{3}{11}+\frac{3}{5}\right)\)
= \(\left(\frac{2}{7}-\frac{2}{11}+\frac{2}{5}\right):\left(\frac{3}{7}-\frac{3}{11}+\frac{3}{5}\right)\)
= \(2\left(\frac{1}{7}-\frac{1}{11}+\frac{1}{5}\right):3\left(\frac{1}{7}-\frac{1}{11}+\frac{1}{5}\right)\)
= 2:3
= \(\frac{2}{3}\)
b/ \(\frac{0,125-\frac{1}{5}+\frac{1}{7}}{0,375-\frac{3}{5}+\frac{3}{7}}+\frac{\frac{1}{2}+\frac{1}{3}-0,2}{\frac{3}{4}+0,5-\frac{3}{10}}\)
= \(\frac{\frac{1}{8}-\frac{1}{5}+\frac{1}{7}}{\frac{3}{8}-\frac{3}{5}+\frac{3}{7}}+\frac{\frac{1}{2}+\frac{1}{3}-\frac{1}{5}}{\frac{3}{4}+\frac{3}{6}-\frac{3}{10}}\)
= \(\frac{\frac{1}{8}-\frac{1}{5}+\frac{1}{7}}{3\left(\frac{1}{8}-\frac{1}{5}+\frac{1}{7}\right)}+\frac{\frac{1}{2}+\frac{1}{3}-\frac{1}{5}}{\frac{3}{2}\left(\frac{1}{2}+\frac{1}{3}-\frac{1}{5}\right)}\)
= \(\frac{1}{3}+\frac{1}{\frac{3}{2}}\)
= \(\frac{1}{3}+\frac{2}{3}\)
= 1





 giúp mình với ạ câu nào cũng được ạ
giúp mình với ạ câu nào cũng được ạ
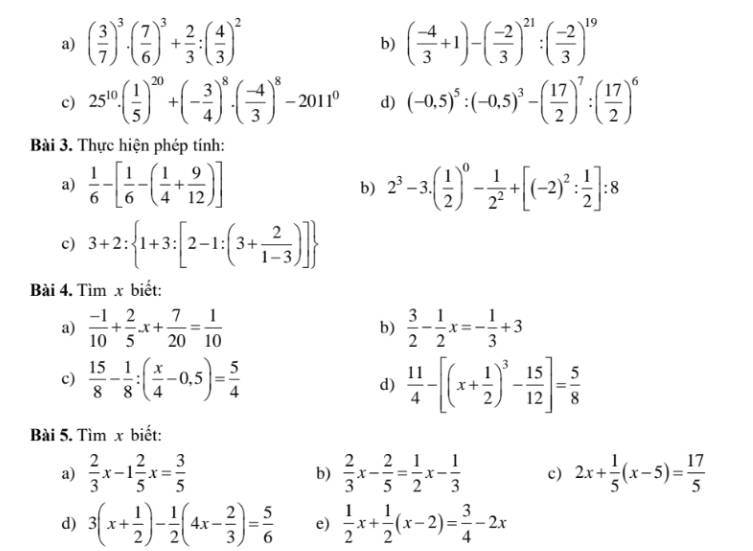

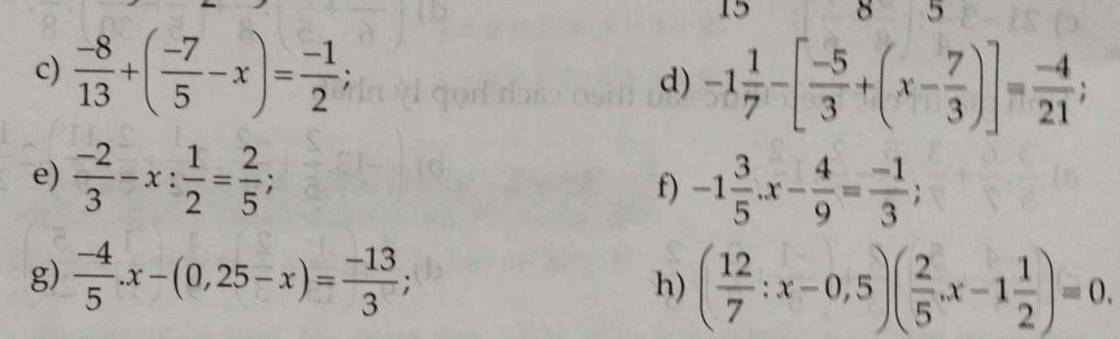


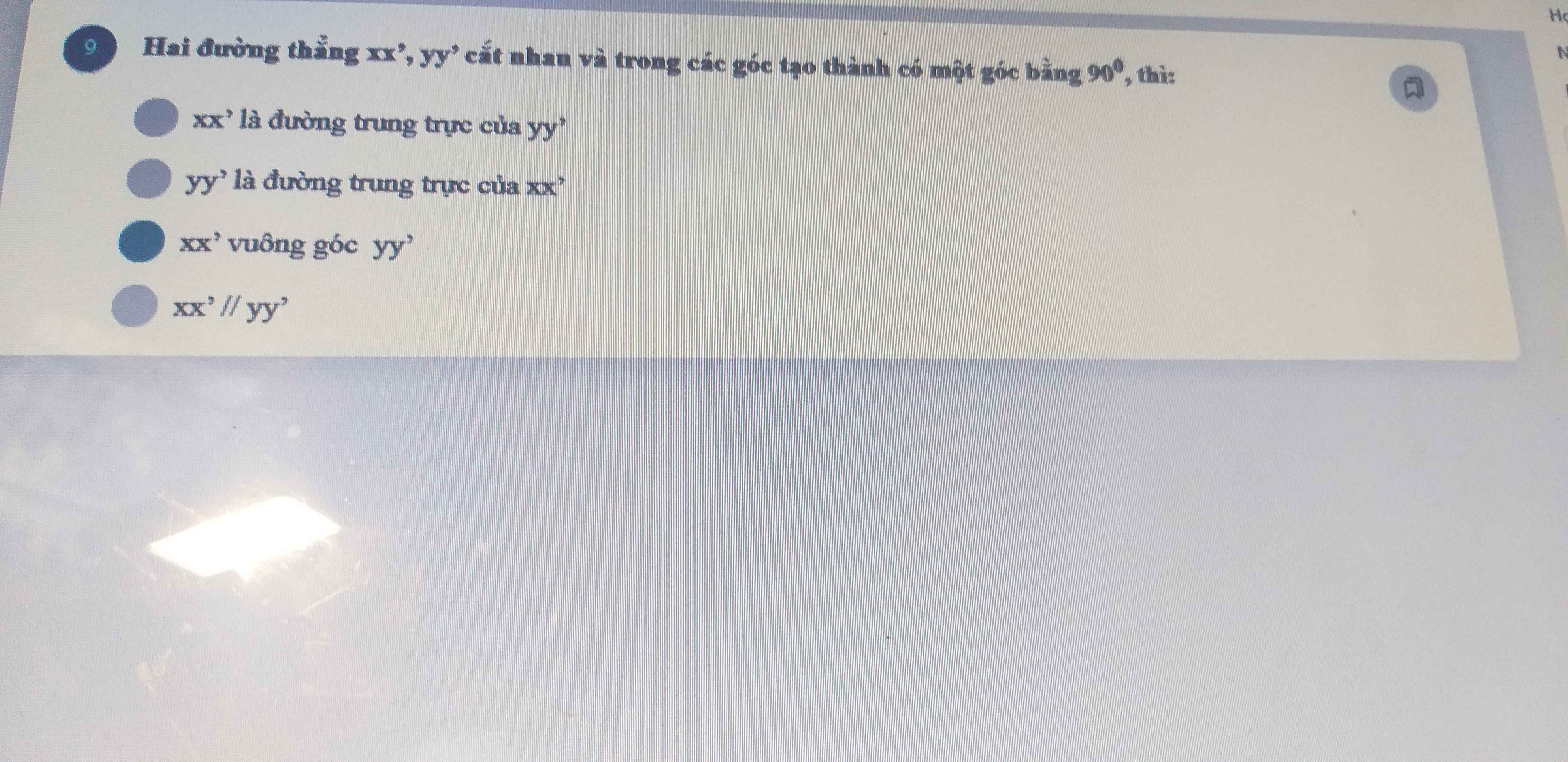
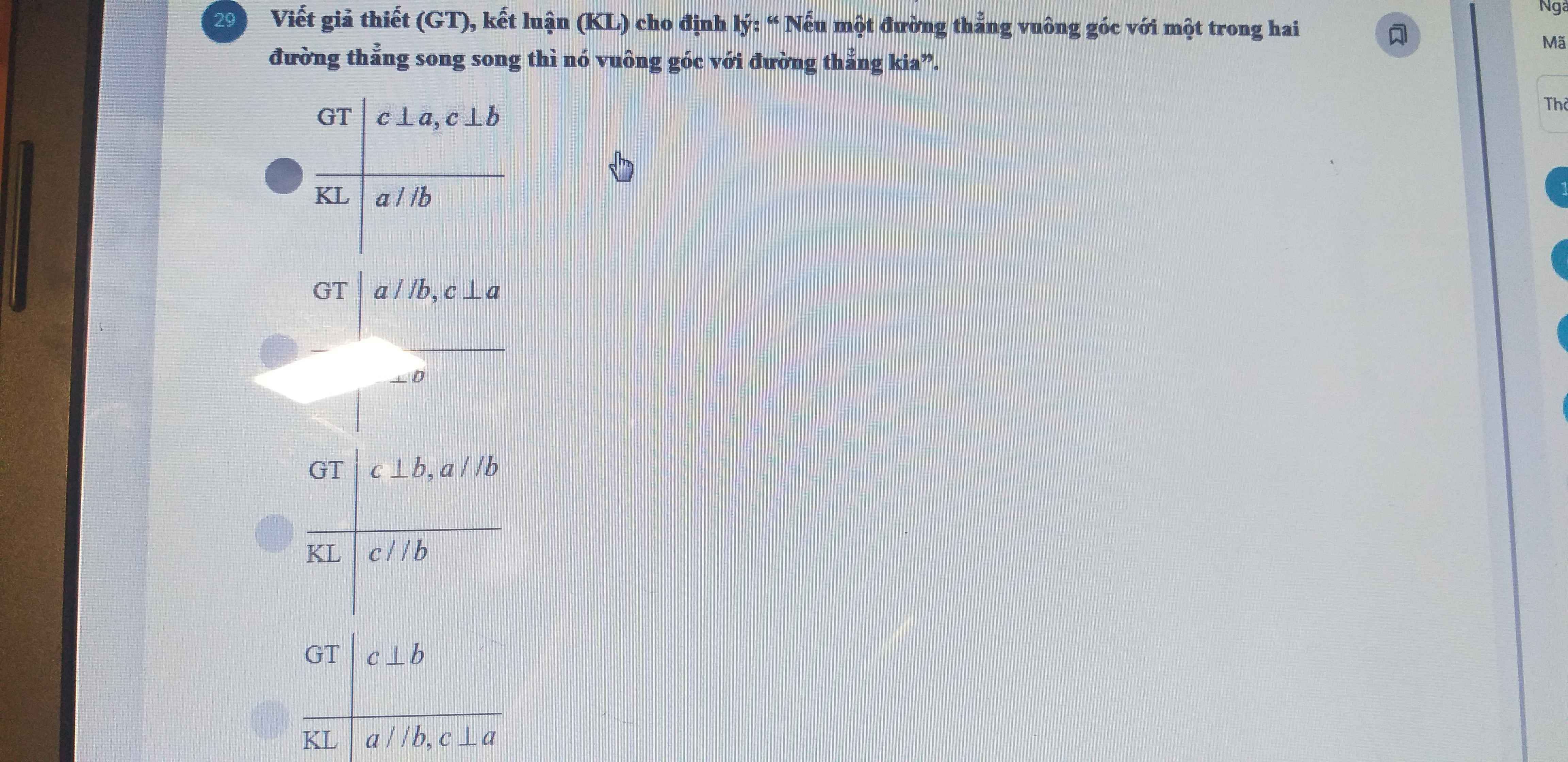



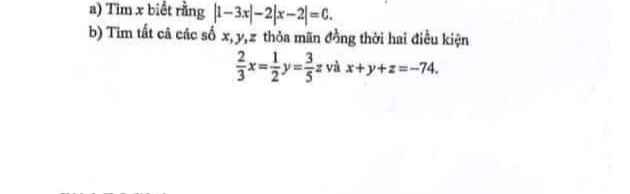

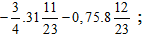 giúp mình với ạ
giúp mình với ạ
