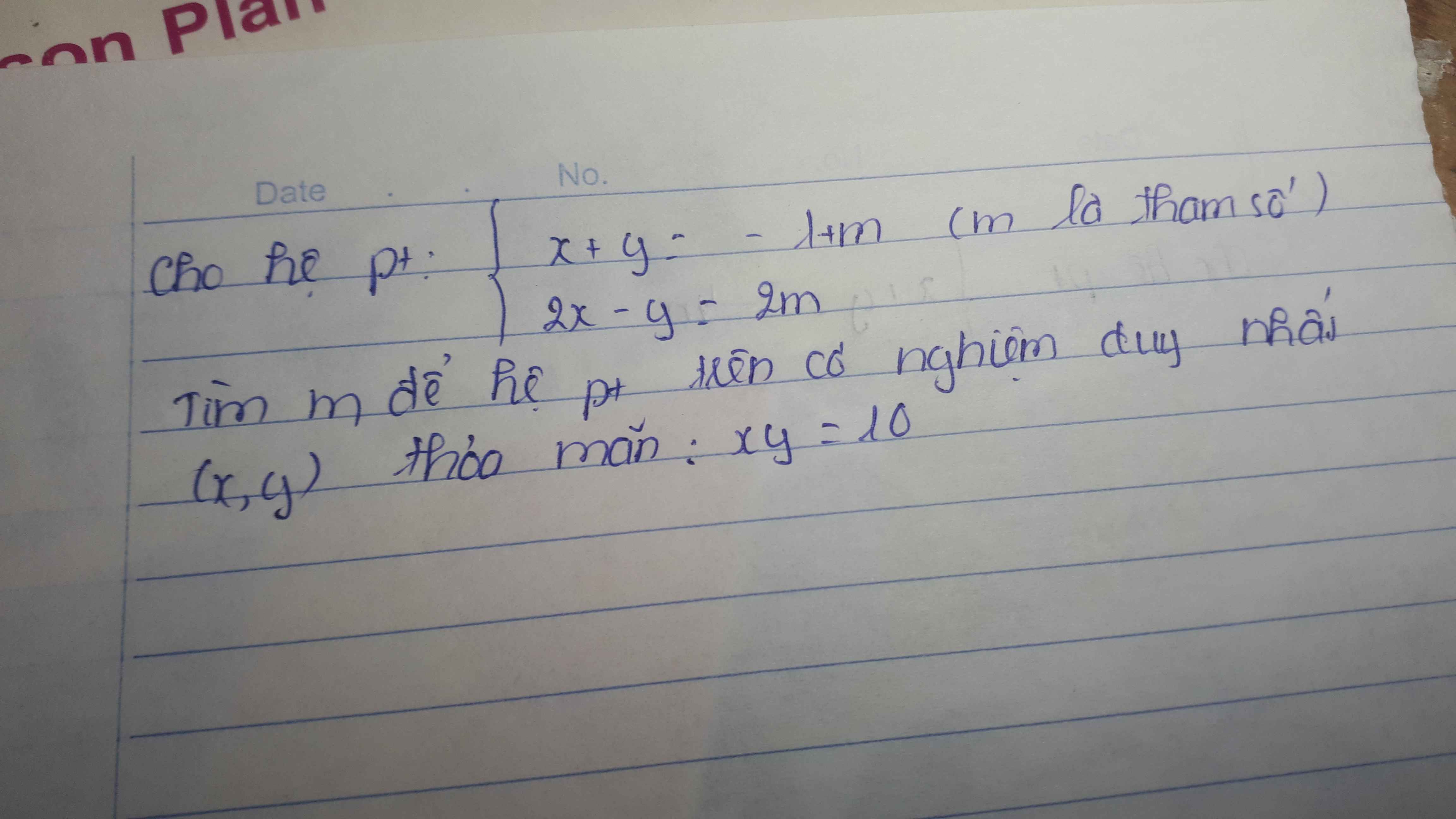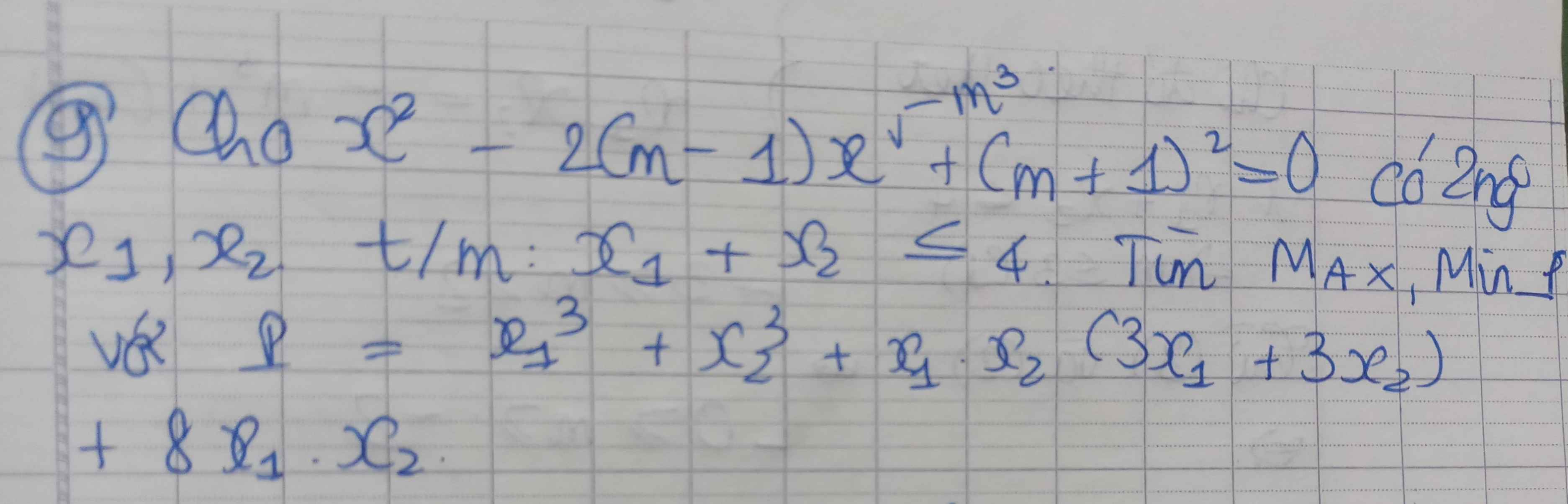\(\Delta'=\left[-\left(m-3\right)\right]^2-3\left(-2m+3\right)\)
\(=m^2-6m+9+6m-9\)
\(=m^2\ge0\forall m\)
Theo Vi - ét:
\(\left\{{}\begin{matrix}x_1+x_2=2m-6\\x_1x_2=-2m+3\end{matrix}\right.\)
\(P=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(2m-6\right)^2-2\left(-2m+3\right)\)
\(=4m^2-24m+36+4m-6\)
\(=4m^2-20m+30\)
\(=4\left(m^2-5m+6\right)\)
\(=4\left(m^2-5m+\dfrac{25}{4}-\dfrac{1}{4}\right)\)
\(=4\left(m-\dfrac{5}{2}\right)^2-1\ge-1\)
Vậy \(Min_P=-1\) khi \(\left(m-\dfrac{5}{2}\right)^2=0\Leftrightarrow m=\dfrac{5}{2}\)
Vậy \(Min_P=-1\) khi \(m=\dfrac{5}{2}\)
Đúng 2
Bình luận (2)
