TXĐ: D=R, y'=-x2+10x-26=0 < 0 với mọi x.
Vậy hàm số đã cho nghịch biến trên khoảng (-\(\infty\);+\(\infty\)).
Đúng 0
Bình luận (0)
Bài 1: Sự đồng biến và nghịch biến của hàm số
Các câu hỏi tương tự
giup minh voi.
Tìm các giá trị thực của tham số m để hàm số y=x+mcosx nghich biến trên R
1, Chứng minh bất đẳng thức:
\(a+\sqrt{a^2-2a+5}+\sqrt{a-1}\ge3\forall a\ge1\)
2, Giải phương trình:
\(x\left(x^2-3x+3\right)+\sqrt{x+3}=3\)
Mong mọi người giúp mình với ạ!! Mình cảm ơn nhiều!!
Chứng minh các bất đẳng thức sau :
a) \(\tan x>\sin x;0< x< \dfrac{\pi}{2}\)
b) \(1+\dfrac{1}{2}x-\dfrac{x^2}{8}< \sqrt{1+x}< 1+\dfrac{1}{2}x\) với \(0< x< +\infty\)
Chứng minh các bất đẳng thức sau:
a) \(tanx > x (0 < x < \dfrac{\pi}{2})\)
b) \(tanx > x + \dfrac{x^3}{3} (0 < x < \dfrac{\pi}{2})\)
chứng minh công thức :
(x-y)^2=(x+y) ^2-4xy
Xem chi tiết
Vẽ một tam giác ABC có góc A=90 độ, AC=3cm, góc C= 60 độ .Trên tia đối của tia AC lấy điểm D sao cho AD=AC
a, Chúng minh tam giác ABD= tam giác ABC
b,tam giÁC BCD có dạng đặc biệt nào ? Vì sao ?
c, Tính độ dài các đoạn thẳng BC,AB
các bạn giúp mình với ạ !!!
Chứng minh các phương trình sau đây có nghiệm duy nhất
a) \(3\left(\cos x-1\right)+2\sin x+6x=0\)
b) \(4x+\cos x-2\sin x-2=0\)
c) \(-x^3+x^2-3x+2=0\)
d) \(x^5+x^3-7=0\)
Chứng minh rằng hàm số 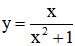đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
Đọc tiếp
Chứng minh rằng hàm số 
đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).
Chứng minh: tanx < \(\dfrac{4}{\pi}x,\forall x\in\left(0;\dfrac{\pi}{4}\right)\)