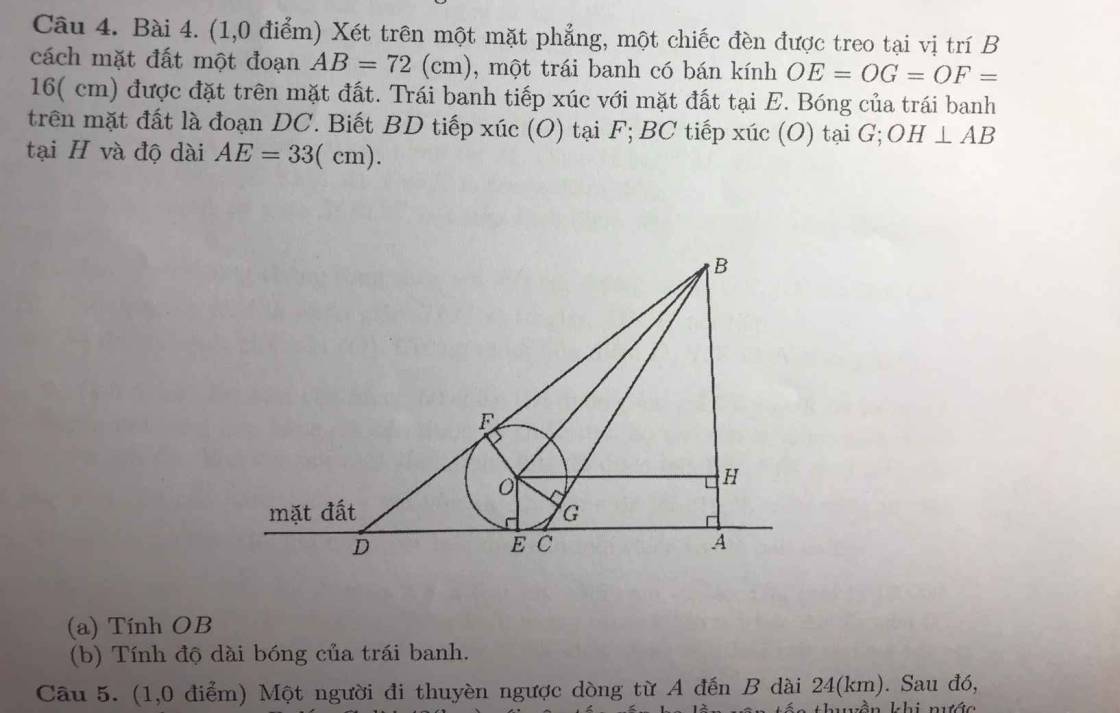
(a) Dễ thấy \(OHAE\) là hình chữ nhật nên : \(AH=OE=16\left(cm\right)\) và \(AE=OH=33\left(cm\right).\)
\(\Rightarrow BH=AB-AH=72-16=56\left(cm\right).\)
Xét \(\Delta OHB\) vuông tại \(H:\)
\(OB^2=OH^2+BH^2\left(Pytago\right)\)
\(\Rightarrow OB=\sqrt{OH^2+BH^2}=\sqrt{33^2+56^2}=65\left(cm\right).\)
Vậy : \(OB=65\left(cm\right).\)
(b) Xét \(\Delta OGB\) vuông tại \(G:\)
\(OB^2=OG^2+BG^2\left(Pytago\right)\)
\(\Rightarrow BG=\sqrt{OB^2-OG^2}=\sqrt{65^2-16^2}=63\left(cm\right)=BF.\)
(tính chất hai tiếp tuyến cắt nhau)
Xét \(\Delta ABC\) vuông tại
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Leftrightarrow\left(BG+CG\right)^2=AB^2+\left(AE-EC\right)^2\)
\(\Leftrightarrow\left(63+CE\right)^2=72^2+\left(33-CE\right)^2\)
(tính chất hai tiếp tuyến cắt nhau)
\(\Rightarrow CE=12\left(cm\right).\)
Xét \(\Delta ADB\) vuông tại \(A:\)
\(BD^2=AD^2+AB^2\left(Pytago\right)\)
\(\Leftrightarrow\left(BF+DF\right)^2=\left(AE+DE\right)^2+AB^2\)
\(\Leftrightarrow\left(63+DE\right)^2=\left(33+DE\right)^2+72^2\)
(tính chất hai tiếp tuyến cắt nhau)
\(\Leftrightarrow DE=38,4\left(cm\right).\)
Độ dài bóng : \(CD=DE+CE=38,4+12=50,4\left(cm\right).\)
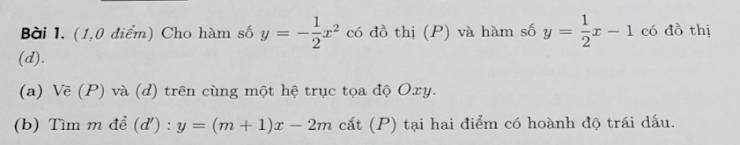giúp mình câu này với ạ