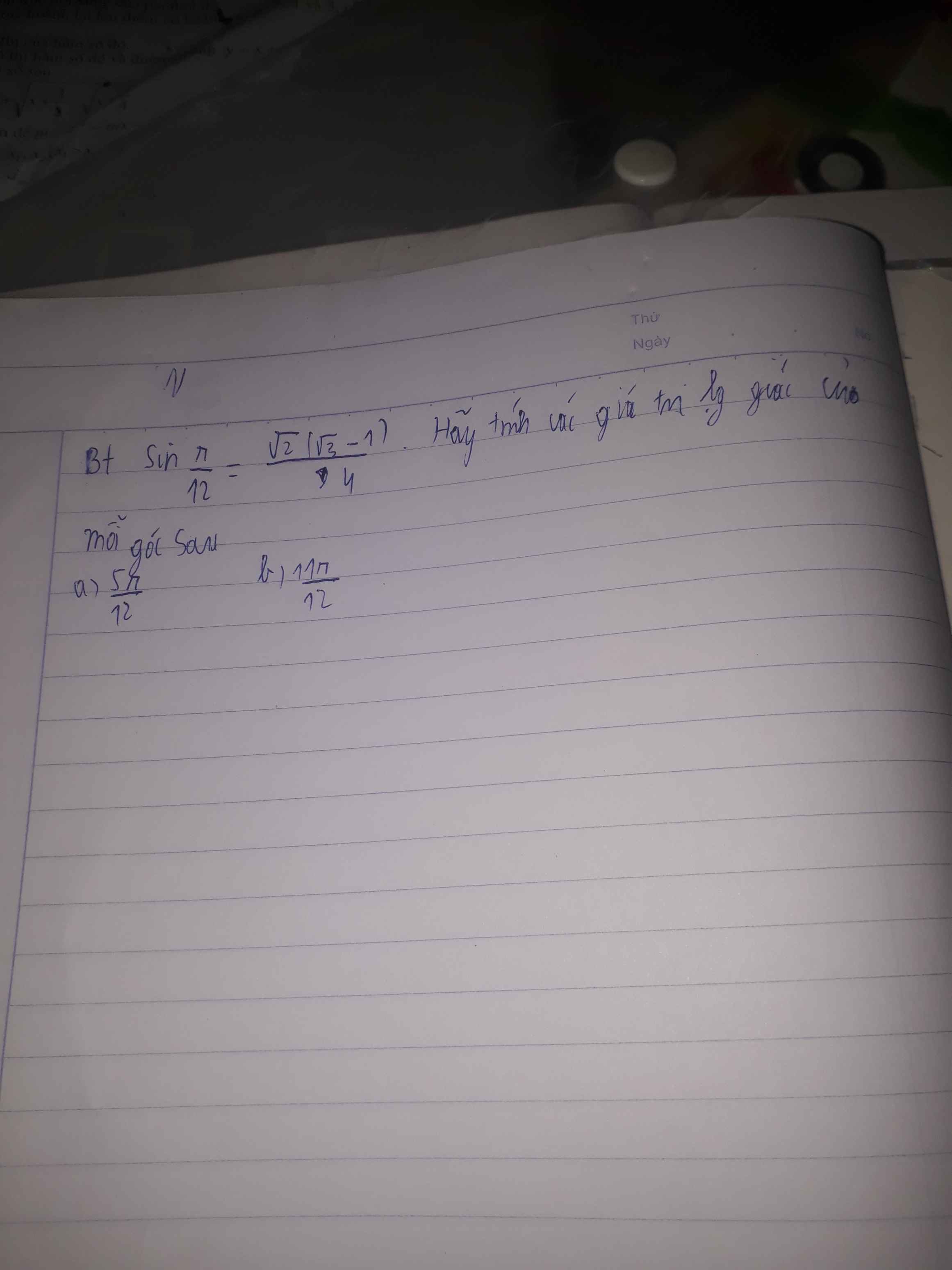\(cos\left(\dfrac{5\pi}{12}\right)=sin\left(\dfrac{\pi}{2}-\dfrac{5\pi}{12}\right)=sin\left(\dfrac{\pi}{12}\right)=\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{4}\)
Lại có \(0< \dfrac{5\pi}{12}< \dfrac{\pi}{2}\Rightarrow sin\left(\dfrac{5\pi}{12}\right)>0\)
\(\Rightarrow sin\left(\dfrac{5\pi}{12}\right)=\sqrt{1-cos^2\left(\dfrac{5\pi}{12}\right)}=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}\)
\(tan\left(\dfrac{5\pi}{12}\right)=\dfrac{sin\left(\dfrac{5\pi}{12}\right)}{cos\left(\dfrac{5\pi}{12}\right)}=2+\sqrt{3}\)
b.
\(sin\left(\dfrac{11\pi}{12}\right)=sin\left(\pi-\dfrac{\pi}{12}\right)=sin\left(\dfrac{\pi}{12}\right)=\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{4}\)
\(cos\left(\dfrac{11\pi}{12}\right)=sin\left(\dfrac{\pi}{2}-\dfrac{11\pi}{12}\right)=sin\left(-\dfrac{5\pi}{12}\right)=-sin\left(\dfrac{5\pi}{12}\right)=-\dfrac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}\)
\(tan\left(\dfrac{11\pi}{12}\right)=\dfrac{sin\left(\dfrac{11\pi}{12}\right)}{cos\left(\dfrac{11\pi}{12}\right)}=-2+\sqrt{3}\)