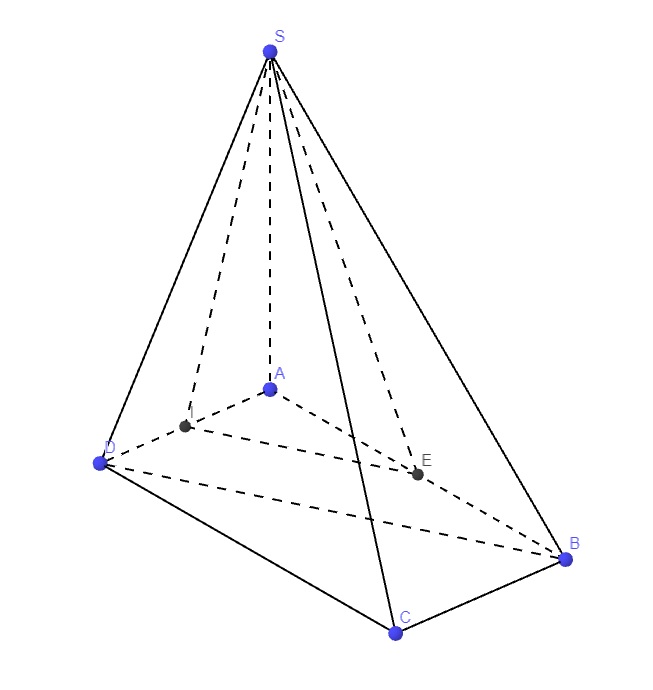
1.
a. Do \(AD||BC\Rightarrow\left(SD;BC\right)=\left(SD;AD\right)=\widehat{SDA}\)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là trung điểm AB \(\Rightarrow IE\) là đường trung bình tam giác ABD
\(\Rightarrow IE||BD\Rightarrow\left(SI;BD\right)=\left(SI;IE\right)=\widehat{SIE}\)
\(IE=\dfrac{1}{2}BD=\dfrac{1}{2}\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{5}}{2}\)
\(SI=\sqrt{SA^2+IA^2}=\sqrt{SA^2+\left(\dfrac{AD}{2}\right)^2}=\dfrac{a\sqrt{13}}{2}\)
\(SE=\sqrt{SA^2+AE^2}=\sqrt{SA^2+\left(\dfrac{AB}{2}\right)^2}=2a\)
Áp dụng định lý hàm cos trong tam giác SIE:
\(cos\widehat{SIE}=\dfrac{SI^2+IE^2-SE^2}{2SI.IE}=\dfrac{\sqrt{65}}{65}\)
\(\Rightarrow\widehat{SIE}\approx82^052'\)
2.
a.
\(BB'||AA'\Rightarrow\left(A'D;BB'\right)=\left(A'D;AA'\right)=\widehat{DA'A}\)
\(tan\widehat{DA'A}=\dfrac{DA}{AA'}=\dfrac{2}{\sqrt{5}}\Rightarrow\widehat{DA'A}\approx41^048'\)
b.
\(CD||AB\Rightarrow\left(AC';CD\right)=\left(AC';AB\right)=\widehat{BAC'}\)
\(AC'=\sqrt{AB^2+AD^2+A'A^2}=a\sqrt{10}\)
\(BC'=\sqrt{AD^2+A'A^2}=3a\)
Áp dụng định lý hàm cos cho tam giác BAC':
\(cos\widehat{BAC'}=\dfrac{AC'^2+AB^2-BC'^2}{2AC'.AB}=\dfrac{\sqrt{10}}{10}\)
\(\Rightarrow\widehat{BAC'}\approx71^034'\)